题目内容
13.在平面直角坐标系xoy中,已知直线l:ax+y+3=0,点A(0,2),若直线l上存在点M,满足|MA|2+|MO|2=10,则实数a的取值范围是{a|$a≤-\sqrt{3}$或$a≥\sqrt{3}$}.分析 设M(x,-ax-3),由已知条件利用两点间距离公式得x2+(-ax-5)2+x2+(-ax-3)2=10,由此利用根的判别式能求出实数a的取值范围.
解答 解:设M(x,-ax-3),
∵直线l:ax+y+3=0,点A(0,2),直线l上存在点M,满足|MA|2+|MO|2=10,
∴x2+(-ax-5)2+x2+(-ax-3)2=10,
整理,得(a2+1)x2+8ax+12=0,
∵直线l上存在点M,满足|MA|2+|MO|2=10,
∴(a2+1)x2+8ax+12=0有解,
∴△=(8a)2-4×12×(a2+1)>0,
解得a$≤-\sqrt{3}$,或a$≥\sqrt{3}$.
故答案为:{a|$a≤-\sqrt{3}$或$a≥\sqrt{3}$}.
点评 本题考查实数的取值范围的求法,是中档题,解题时要认真审题,注意两点间距离公式和一元二次方程式根的判别式的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.直线3x+4y=b与圆x2+y2-2x-2y+1=0相切,则b=( )
| A. | -2或12 | B. | 2或-12 | C. | -2或-12 | D. | 2或12 |
 已知函数f(x)=ax3+bx2+(c-3a-2b)x+d(a>0)的图象如图.
已知函数f(x)=ax3+bx2+(c-3a-2b)x+d(a>0)的图象如图.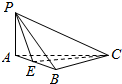 如图,三棱锥P-ABC中,△PAB是正三角形,E是AB的中点,AB⊥BC,平面PAB⊥平面ABC.若AB=2,BC=$\sqrt{2}$,则点A到平面PEC的距离是$\frac{\sqrt{6}}{3}$.
如图,三棱锥P-ABC中,△PAB是正三角形,E是AB的中点,AB⊥BC,平面PAB⊥平面ABC.若AB=2,BC=$\sqrt{2}$,则点A到平面PEC的距离是$\frac{\sqrt{6}}{3}$.