题目内容
已知锐角△ABC内有一点O,满足OA=OB=OC,且∠A=60°,若 =
= ,则m等于
,则m等于
- A.

- B.

- C.

- D.无法确定
B
分析:把已知式两边同时乘以 ,设 OA=OB=OC=R,由于∠AOB=2C,∠AOC=2B,可得
,设 OA=OB=OC=R,由于∠AOB=2C,∠AOC=2B,可得  +
+ =-2mR2,由 m=sinBcosC+sinCcosB=sin(B+C)=sinA 求得结果.
=-2mR2,由 m=sinBcosC+sinCcosB=sin(B+C)=sinA 求得结果.
解答:∵ =
= ,
,
∴ =2m
=2m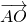 ,
,
两边同时乘以 可得
可得  •
• =2m
=2m 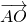 •
• .
.
设 OA=OB=OC=R,由于∠AOB=2C,∠AOC=2B,
∴ +
+ =-2mR2,
=-2mR2,
∴m=sinBcosC+sinCcosB=sin(B+C)=sinA= ,
,
故选B.
点评:本题主要考查两个向量的加减法的法则,以及其几何意义,诱导公式的应用,属于中档题.
分析:把已知式两边同时乘以
 ,设 OA=OB=OC=R,由于∠AOB=2C,∠AOC=2B,可得
,设 OA=OB=OC=R,由于∠AOB=2C,∠AOC=2B,可得  +
+ =-2mR2,由 m=sinBcosC+sinCcosB=sin(B+C)=sinA 求得结果.
=-2mR2,由 m=sinBcosC+sinCcosB=sin(B+C)=sinA 求得结果.解答:∵
 =
= ,
,∴
 =2m
=2m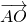 ,
,两边同时乘以
 可得
可得  •
• =2m
=2m 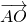 •
• .
.设 OA=OB=OC=R,由于∠AOB=2C,∠AOC=2B,
∴
 +
+ =-2mR2,
=-2mR2,∴m=sinBcosC+sinCcosB=sin(B+C)=sinA=
 ,
,故选B.
点评:本题主要考查两个向量的加减法的法则,以及其几何意义,诱导公式的应用,属于中档题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 +
+ =2 m
=2 m ,则m等于
,则m等于