题目内容
19．
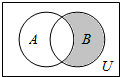设全集U=R，集合A={x|$\frac{x-3}{x+2}$=0}，B={x|x2-x-6=0}，则阴影部分所表示的集合是（ ）| A． | {3} | B． | {-2} | C． | {3，-2} | D． | {∅} |
分析 由图象可知阴影部分对应的集合为B∩（∁UA），然后根据集合的基本运算求解即可．
解答 解：由Venn图可知阴影部分对应的集合为B∩（∁UA），
∵集合A={x|$\frac{x-3}{x+2}$=0}={3}，B={x|x2-x-6=0}={-2，3}，
∴B∩（∁UA）={-2}，
故选：B．
点评 本题主要考查集合的基本运算，利用图象先确定集合关系是解决本题的关键，比较基础．
练习册系列答案
英才点津系列答案
红果子三级测试卷系列答案
相关题目
10．已知函数f（x）=sin（ωx+$\frac{π}{6}$）（ω＞0）的最小正周期为π，则该函数的图象（ ）
| A． | 关于直线x=$\frac{π}{6}$对称 | B． | 关于直线x=$\frac{π}{4}$对称． | ||
| C． | 关于点（$\frac{π}{4}$，0）对称 | D． | 关于点（$\frac{π}{6}$，0）对称 |
4．已知函数f（x）=$\frac{{x}^{2}+x+1}{{x}^{2}+1}$，若f（a）=$\frac{4}{3}$，则f（-a）=（ ）
| A． | $\frac{2}{3}$ | B． | -$\frac{2}{3}$ | C． | $\frac{4}{3}$ | D． | -$\frac{4}{3}$ |