题目内容
11.已知二次函数f(x)与函数y=-2(x+1)2的开口大小相同,开口方向也相同,f(x)的图象的顶点是(1,2),定义在R上的函数g(x)是奇函数,当x>0时,g(x)=f(x).(1)求函数g(x)的解析式;
(2)作出函数g(x)的图象,并说明g(x)的单调性.
分析 (1)根据图象的特点,先求出f(x)的解析式,根据函数奇偶性的性质,将x<0转化为-x>0,即可求出函数的解析式.
(2)画图,由图象得到单调性.
解答 解:(1)由题知:f(x)=-2(x+1)2+2,
当x>0时,g(x)=f(x)=-2x2+4x,
∵g(x)是奇函数,
∴g(-x)=-g(x),
当x=0时,g(-0)=-g(0),
∴g(0)=0,
当x<0时,则-x>0,
∴g(-x)=-2x2-4x=-g(x),
∴g(x)=2x2+4x,
∴g(x)=$\left\{\begin{array}{l}{2{x}^{2}+4x,x<0}\\{-2{x}^{2}+4x,x≥0}\end{array}\right.$;
(2)图象如图所示: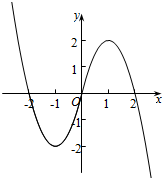
由图象可知,g(x)在[-1,1]上单调递增,在(-∞,-1),(1,+∞)是单调递减.
点评 本题主要考查函数解析式的求法以及函数的图象的识别,利用函数的奇偶性的性质是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.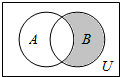 设全集U=R,集合A={x|$\frac{x-3}{x+2}$=0},B={x|x2-x-6=0},则阴影部分所表示的集合是( )
设全集U=R,集合A={x|$\frac{x-3}{x+2}$=0},B={x|x2-x-6=0},则阴影部分所表示的集合是( )
 设全集U=R,集合A={x|$\frac{x-3}{x+2}$=0},B={x|x2-x-6=0},则阴影部分所表示的集合是( )
设全集U=R,集合A={x|$\frac{x-3}{x+2}$=0},B={x|x2-x-6=0},则阴影部分所表示的集合是( )| A. | {3} | B. | {-2} | C. | {3,-2} | D. | {∅} |
16.已知△ABC的两边长分别为2,3,这两边的夹角的余弦值为$\frac{1}{3}$,则△ABC的外接圆的直径为( )
| A. | $\frac{9\sqrt{2}}{2}$ | B. | $\frac{9\sqrt{2}}{4}$ | C. | $\frac{9\sqrt{2}}{6}$ | D. | 8$\sqrt{2}$ |
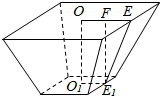 已知正四棱台高是12cm,两底面边长之差为10cm,全面积为512cm2.
已知正四棱台高是12cm,两底面边长之差为10cm,全面积为512cm2.