题目内容
4.已知函数f(x)=$\frac{{x}^{2}+x+1}{{x}^{2}+1}$,若f(a)=$\frac{4}{3}$,则f(-a)=( )| A. | $\frac{2}{3}$ | B. | -$\frac{2}{3}$ | C. | $\frac{4}{3}$ | D. | -$\frac{4}{3}$ |
分析 由已知得f(a)=1+$\frac{a}{{a}^{2}+1}$=$\frac{4}{3}$,由此利用f(-a)=1-$\frac{a}{{a}^{2}+1}$,能求出结果.
解答 解:∵函数f(x)=$\frac{{x}^{2}+x+1}{{x}^{2}+1}$=1+$\frac{x}{{x}^{2}+1}$,
∴f(a)=1+$\frac{a}{{a}^{2}+1}$=$\frac{4}{3}$,
解得$\frac{a}{{a}^{2}+1}$=$\frac{1}{3}$,
∴f(-a)=1-$\frac{a}{{a}^{2}+1}$=$\frac{2}{3}$.
故选:A.
点评 本题考查函数值的求法,是基础题,解题时要注意函数性质的合理运用.

练习册系列答案
相关题目
15.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+3x(x≥0)}\\{g(x)(x<0)}\end{array}\right.$为奇函数,则f(g(-1))=( )
| A. | -28 | B. | -8 | C. | -4 | D. | 4 |
12.若曲线y=e-x上点P处的切线垂直于直线x-2y+1=0,则点P的坐标是( )
| A. | (-2,ln2) | B. | (2,-ln2) | C. | (-ln2,2) | D. | (ln2,-2) |
19.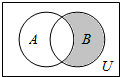 设全集U=R,集合A={x|$\frac{x-3}{x+2}$=0},B={x|x2-x-6=0},则阴影部分所表示的集合是( )
设全集U=R,集合A={x|$\frac{x-3}{x+2}$=0},B={x|x2-x-6=0},则阴影部分所表示的集合是( )
 设全集U=R,集合A={x|$\frac{x-3}{x+2}$=0},B={x|x2-x-6=0},则阴影部分所表示的集合是( )
设全集U=R,集合A={x|$\frac{x-3}{x+2}$=0},B={x|x2-x-6=0},则阴影部分所表示的集合是( )| A. | {3} | B. | {-2} | C. | {3,-2} | D. | {∅} |
16.已知△ABC的两边长分别为2,3,这两边的夹角的余弦值为$\frac{1}{3}$,则△ABC的外接圆的直径为( )
| A. | $\frac{9\sqrt{2}}{2}$ | B. | $\frac{9\sqrt{2}}{4}$ | C. | $\frac{9\sqrt{2}}{6}$ | D. | 8$\sqrt{2}$ |