题目内容

10．化简cos4$θ-\frac{1}{4}co{s}^{2}2θ-\frac{1}{2}cos2θ$=$\frac{1}{4}$．

分析 由条件利用二倍角的余弦公式，完全平方公式化简所给的式子，可得结果．

解答 解：cos4$θ-\frac{1}{4}co{s}^{2}2θ-\frac{1}{2}cos2θ$=（cos2θ）2-$\frac{1}{4}$cos22θ-$\frac{1}{2}$cos2θ=${（\frac{1+cos2θ}{2}）}^{2}$-$\frac{1}{4}$cos22θ-$\frac{1}{2}$cos2θ
=$\frac{1}{4}$cos22θ+$\frac{1}{2}$cos2θ+$\frac{1}{4}$-$\frac{1}{4}$cos22θ-$\frac{1}{2}$cos2θ=$\frac{1}{4}$，
故答案为：$\frac{1}{4}$．

点评 本题主要考查二倍角的余弦公式，完全平方公式，属于基础题．

练习册系列答案
相关题目
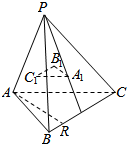20．如图，P是△ABC所在平面外的一点，A1，B1，C1依次是△PBC，△PAC，△PAB的重心，AR是平面ABC内的任意一条直线，求证：AR∥平面A1B1C1．
1．求函数f（x）=3|x|的单调区间．
18．已知二次函数f（x）=ax2+bx+c（a≠0）的图象过点（-1，0），命题p：对任意实数x，f（x）≥x；命题q：存在实数x，使f（x）＞$\frac{1}{2}$（x2+1）若命题“p且非q”为真命题．
（1）求证：f（1）=1；
（2）求f（x）的解析式．
5．设$α=\frac{17}{3}π$，则（　　）
A．sinα＞0，cosα＞0B．sinα＜0，cosα＜0C．sinα＞0，cosα＜0D．sinα＜0，cosα＞0
15．M是抛物线y2=2x上-点，P点坐标为（3，$\frac{10}{3}$），设d是点M到准线的距离，要使d+|MP|最小，则点M的坐标为（2，2）．
2．不共线三点A、B、P∉平面α，点P∉直线AB，AP∩α=A1，BP∩α=B1，AB∩α=O，当点P在空间中变动时，定点O与动直线A1B1的位置关系是O∈A1B1．
19．函数f（x）=ax2-2014x+2015（a＞0），在区间[t-1，t+1]（t∈R）上函数f（x）的最大值为M，最小值为N，当t取任意实数时．M-N的最小值为1，则a=（　　）
A．1B．2C．3D．4
20．若f（x）是定义在R上的偶函数，且满足f（x）=-f（x+$\frac{3}{2}$），f（-1）=1，f（0）=-2，则f（1）+f（2）+…+f（2008）的值为（　　）
A．-2B．0C．1D．2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网