题目内容
设关于x的二次方程x2+(m-1)x+1=0在区间[0,2]上有两不同解,则实数m的取值范围是
[-
,-1),
| 3 |
| 2 |
[-
,-1),
.| 3 |
| 2 |
分析:将方程转化为函数f(x)=x2+(m-1)x+1,利用二次函数根的分布,确定m的取值范围.
解答: 解:设f(x)=x2+(m-1)x+1,要使方程x2+(m-1)x+1=0在区间[0,2]上有两不同解,
解:设f(x)=x2+(m-1)x+1,要使方程x2+(m-1)x+1=0在区间[0,2]上有两不同解,
则对应函数f(x)满足
,即
,
解得-
≤m<-1,所以实数m的取值范围是[-
,-1).
故答案为:[-
,-1).
 解:设f(x)=x2+(m-1)x+1,要使方程x2+(m-1)x+1=0在区间[0,2]上有两不同解,
解:设f(x)=x2+(m-1)x+1,要使方程x2+(m-1)x+1=0在区间[0,2]上有两不同解,则对应函数f(x)满足
|
|
解得-
| 3 |
| 2 |
| 3 |
| 2 |
故答案为:[-
| 3 |
| 2 |
点评:本题主要考查二次方程根的取值,将二次转化为函数,利用二次函数根的分布是解决此类问题的关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
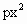 +(p-1)x+p+1=0有两个不等的正根,且一根大于另一根的两倍,求p的取值范围.
+(p-1)x+p+1=0有两个不等的正根,且一根大于另一根的两倍,求p的取值范围. 是等比数列;
是等比数列; 时,求数列{an}的通项公式.
时,求数列{an}的通项公式.