题目内容
【题目】已知数列
的各项均为正数，
，且对任意
,都有
，数列前n项的和
.
（1）若数列是等比数列，求
的值和
；
（2）若数列是等差数列，求
和的关系式；
（3）
，当
时，求证: 
是一个常数.
【答案】（1）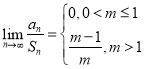
； （2）
； （3）见解析.
【解析】
（1）确定数列的通项，利用
，可得c的值，分类讨论求和可得
；
（2）求出数列的公差，利用，建立关系式，可得
和
的关系式；
（3）利用分析法进行证明.
（1）由题意得：
，
，
因为数列
的各项均为正数，所以
当
时，
，
，
当且
时，
，
当
时，
当
时，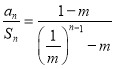
，
所以
（2）由题意得：
，
，
，
（3）计算
，
猜想
欲证明恒成立
只需要证明
恒成立
即要证明
恒成立
即要证明
恒成立（***）
，
，
（***）左边
（***）右边
所以（***）成立
方法二：计算
猜想
，
由于
，上式两边同除以
，
得
.
所以，
.
所以是常数
练习册系列答案
相关题目
