题目内容
【题目】已知数列![]() 的前n项和为
的前n项和为![]() ,且满足
,且满足![]() ,数列
,数列![]() 中,
中,![]() ,对任意正整数
,对任意正整数![]() ,
, .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)是否存在实数![]() ,使得数列
,使得数列![]() 是等比数列?若存在,请求出实数
是等比数列?若存在,请求出实数![]() 及公比q的值,若不存在,请说明理由;
及公比q的值,若不存在,请说明理由;
(3)求数列![]() 前n项和
前n项和![]() .
.
【答案】(1)![]()
(2)存在,![]() ,
, ![]()
(3)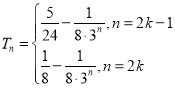 (
(![]() )
)
【解析】
(1)根据![]() 与
与![]() 的关系
的关系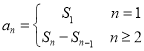 即可求出;
即可求出;
(2)假设存在实数![]() ,利用等比数列的定义列式,与题目条件
,利用等比数列的定义列式,与题目条件![]() ,比较对应项系数即可求出
,比较对应项系数即可求出![]() ,即说明存在这样的实数;
,即说明存在这样的实数;
(3)由(2)可以求出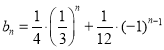 ,所以根据分组求和法和分类讨论法即可求出.
,所以根据分组求和法和分类讨论法即可求出.
(1)因为![]() ,
,
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
故![]() ;
;
(2)假设存在实数![]() ,使得数列
,使得数列![]() 是等比数列,数列
是等比数列,数列![]() 中,
中,![]() ,
,
对任意正整数![]() ,
,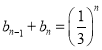 .可得
.可得![]() ,且
,且![]() ,
,
由假设可得![]() ,即
,即![]() ,
,
则![]() ,可得
,可得![]() ,
,
可得存在实数![]() ,使得数列
,使得数列![]() 是公比
是公比![]() 的等比数列;
的等比数列;
(3)由(2)可得![]() ,则
,则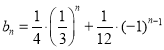 ,
,
则前n项和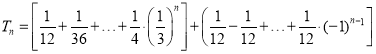
当n为偶数时,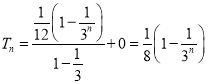
当n为奇数时,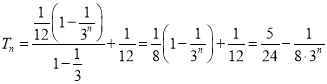
则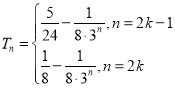 (
(![]() ).
).

【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:千元)对年销售量
(单位:千元)对年销售量![]() (单位:
(单位:![]() )和年利润
)和年利润![]() (单位:千元)的影响,对近8年的宣传费
(单位:千元)的影响,对近8年的宣传费![]() 和年销售量
和年销售量![]() 数据作了初步处理,得到下面的散点图及一些统计量的值.
数据作了初步处理,得到下面的散点图及一些统计量的值.

|
|
|
|
|
|
|
46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
表中![]() ,
,![]()
附:对于一组数据![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
(1)根据散点图判断,![]() 与
与![]() ,哪一个适宜作为年销售量
,哪一个适宜作为年销售量![]() 关于年宣传费
关于年宣传费![]() 的回归方程类型(给出判断即可,不必说明理由);
的回归方程类型(给出判断即可,不必说明理由);
(2)根据(1)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)已知这种产品的年利润![]() 与
与![]() 的关系为
的关系为![]() ,根据(2)的结果回答:当年宣传费
,根据(2)的结果回答:当年宣传费![]() 时,年销售量及年利润的预报值是多少?
时,年销售量及年利润的预报值是多少?
【题目】高中生在被问及“家,朋友聚集的地方,个人空间”三个场所中“感到最幸福的场所在哪里?”这个问题时,从中国某城市的高中生中,随机抽取了55人,从美国某城市的高中生中随机抽取了45人进行答题.中国高中生答题情况是:选择家的占![]() 、朋友聚集的地方占
、朋友聚集的地方占![]() 、个人空间占
、个人空间占![]() .美国高中生答题情况是:朋友聚集的地方占
.美国高中生答题情况是:朋友聚集的地方占![]() 、家占
、家占![]() 、个人空间占
、个人空间占![]() .如下表:
.如下表:
在家里最幸福 | 在其它场所幸福 | 合计 | |
中国高中生 | |||
美国高中生 | |||
合计 |
(Ⅰ)请将![]() 列联表补充完整;试判断能否有
列联表补充完整;试判断能否有![]() 的把握认为“恋家”与否与国别有关;
的把握认为“恋家”与否与国别有关;
(Ⅱ)从被调查的不“恋家”的美国学生中,用分层抽样的方法选出4人接受进一步调查,再从4人中随机抽取2人到中国交流学习,求2人中含有在“个人空间”感到幸福的学生的概率.
附:![]() ,其中
,其中![]() .
.
| 0.050 | 0.025 | 0.010 | 0.001 |
| 3.841 | 5.024 | 6.635 | 10.828 |
【题目】响应“文化强国建设”号召,某市把社区图书阅览室建设增列为重要的民生工程.为了解市民阅读需求,随机抽取市民200人做调查,统计数据表明,样本中所有人每天用于阅读的时间(简称阅读用时)都不超过3小时,其频数分布表如下:(用时单位:小时)
用时分组 |
|
|
|
|
|
|
频数 | 10 | 20 | 50 | 60 | 40 | 20 |
(1)用样本估计总体,求该市市民每天阅读用时的平均值;
(2)为引导市民积极参与阅读,有关部门牵头举办市读书经验交流会,从这200人中筛选出男女代表各3名,其中有2名男代表和1名女代表喜欢古典文学.现从这6名代表中任选2名男代表和2名女代表参加交流会,求参加交流会的4名代表中,喜欢古典文学的男代表多于喜欢古典文学的女代表的概率.