Question

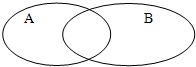记符号A-B={x|x∈A，且x∉B}
（1）如下图所示，用阴影部分表示集合A-B
（2）若A={x|

1

2

＜2x＜4}，B={x|x-1＞0}，求A-B和B-A．

Answer 1

分析：（1）根据已知中A-B={x|x∈A，且x∉B}，我们可得A-B表示，集合A中除去B中所有元素，即除到A，B共公元素之外的元素给成的集合，根据已知中A，B的韦恩图，结合A-B的定义即可用阴部部分表示集合A-B
（2）由已知中A={x|

1

2

＜2x＜4}=（-1，2），B={x|x-1＞0}=（1，+∞），结合A-B的定义，结合集合补集及交集的运算方法易给出答案．

解答：解：（1）根据A-B={x|x∈A，且x∉B}可得A-B如下图所示

（2）若A={x|

1

2

＜2x＜4}=（-1，2），B={x|x-1＞0}=（1，+∞），
则A-B={x|

1

2

＜2x＜4，且x-1≤0}=（-1，1]
B-A={x|

1

2

≥2x，或2x≥4，且x-1＞0}=[2，+∞）

点评：本题考查的知识点是Venn图表达集合的关系及运算，元素与集合关系的判断，其中正确理解集合A-B的定义，准确理解集合A-B中元素的性质是解答本题的关键．