题目内容
已知椭圆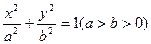 的左右焦点分别为
的左右焦点分别为 ,左顶点为
,左顶点为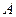 ,若
,若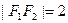 ,椭圆的离心率为
,椭圆的离心率为
(Ⅰ)求椭圆的标准方程,
(Ⅱ)若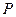 是椭圆上的任意一点,求
是椭圆上的任意一点,求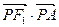 的取值范围
的取值范围
(III)直线 与椭圆相交于不同的两点
与椭圆相交于不同的两点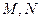 (均不是长轴的顶点),
(均不是长轴的顶点), 垂足为H且
垂足为H且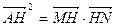 ,求证:直线
,求证:直线 恒过定点.
恒过定点.
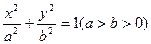 的左右焦点分别为
的左右焦点分别为 ,左顶点为
,左顶点为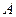 ,若
,若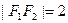 ,椭圆的离心率为
,椭圆的离心率为
(Ⅰ)求椭圆的标准方程,
(Ⅱ)若
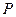 是椭圆上的任意一点,求
是椭圆上的任意一点,求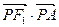 的取值范围
的取值范围(III)直线
 与椭圆相交于不同的两点
与椭圆相交于不同的两点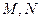 (均不是长轴的顶点),
(均不是长轴的顶点), 垂足为H且
垂足为H且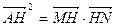 ,求证:直线
,求证:直线 恒过定点.
恒过定点.(Ⅰ)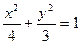 (Ⅱ)
(Ⅱ)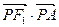 的取值范围是[0,12]
的取值范围是[0,12]
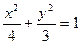 (Ⅱ)
(Ⅱ)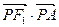 的取值范围是[0,12]
的取值范围是[0,12](I)由题意得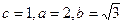
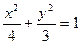 ………………4分
………………4分
(II)设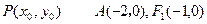
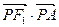
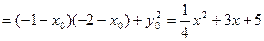
由椭圆方程得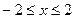 ,二次函数开口向上,对称轴x=-6<-2
,二次函数开口向上,对称轴x=-6<-2
当x=-2时,取最小值0,
当x= 2时, 取最大值12
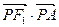 的取值范围是[0,12] ………………………………9分
的取值范围是[0,12] ………………………………9分
(III)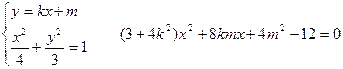
由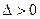 得
得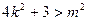 ※网w。w-w*k&s%5¥u
※网w。w-w*k&s%5¥u
设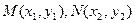 ,则
,则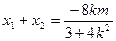 ,
, 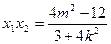
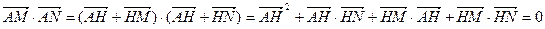 ∴
∴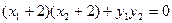
即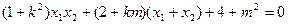
∴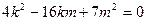
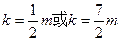 均适合※ ………………12分
均适合※ ………………12分
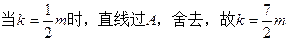
 …………………………13分
…………………………13分
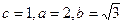
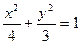 ………………4分
………………4分(II)设
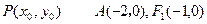
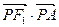
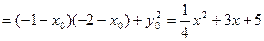
由椭圆方程得
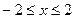 ,二次函数开口向上,对称轴x=-6<-2
,二次函数开口向上,对称轴x=-6<-2当x=-2时,取最小值0,
当x= 2时, 取最大值12
 的取值范围是[0,12] ………………………………9分
的取值范围是[0,12] ………………………………9分(III)
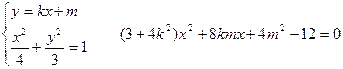
由
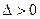 得
得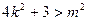 ※网w。w-w*k&s%5¥u
※网w。w-w*k&s%5¥u设
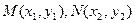 ,则
,则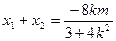 ,
, 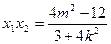
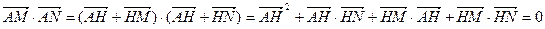 ∴
∴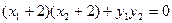
即
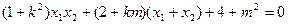
∴
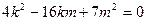
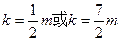 均适合※ ………………12分
均适合※ ………………12分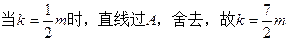
 …………………………13分
…………………………13分
练习册系列答案
相关题目
 轴上,短轴长为4,离心率为
轴上,短轴长为4,离心率为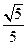 .
. 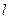 过该椭圆的左焦点,交椭圆于M、N两点,且
过该椭圆的左焦点,交椭圆于M、N两点,且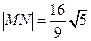 ,求直线
,求直线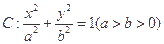 的离心率为
的离心率为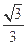 ,过右焦点F的直线
,过右焦点F的直线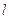 与
与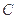 相交于
相交于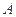 、
、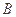 两点,当
两点,当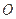 到
到
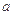 ,
,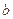 的值;
的值;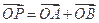 成立?
成立?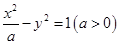 的离心率为
的离心率为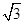 ,则
,则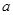 的值是
的值是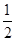
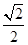
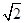
 中,已知椭圆
中,已知椭圆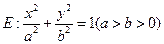 过点
过点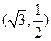 ,且椭圆
,且椭圆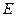 的离心率为
的离心率为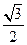 .
.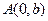 为直角顶点且内接于椭圆
为直角顶点且内接于椭圆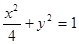 的右焦点,椭圆上的点与点F的最大距离为M,最小距离为N,则椭圆上与点F的距离等于
的右焦点,椭圆上的点与点F的最大距离为M,最小距离为N,则椭圆上与点F的距离等于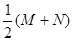 的点的坐标是
的点的坐标是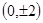
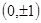
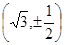
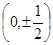
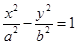 (a>0,b>0)的两个焦点为
(a>0,b>0)的两个焦点为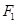 、
、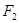 ,点A在双曲线
,点A在双曲线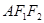 的面积为1,且
的面积为1,且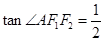 ,
,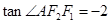 ,则
,则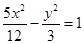

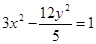
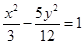
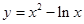 上任意一点,则点P到直线
上任意一点,则点P到直线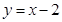 的最小距离为 ( )
的最小距离为 ( )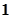
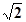
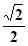
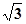
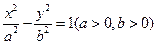 ,过左焦点F1作斜率为
,过左焦点F1作斜率为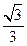 的直线交双曲线的右支于点P,且
的直线交双曲线的右支于点P,且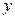 轴平分线段F1P,则双曲线的离心率是
轴平分线段F1P,则双曲线的离心率是