题目内容
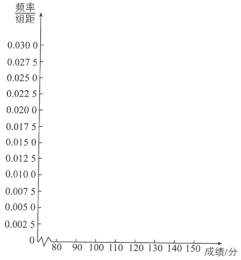
【题目】目前，新型冠状病毒感染的肺炎疫情防控形势严峻.口罩的市场需求一直居高不下.为了保障防疫物资供应，潍坊的口罩企业加足马力保生产，上演了一场与时间赛跑的“防疫阻击战”.潍坊市坊子区一家口罩生产企业拥有1000平方米洁净车间，配备国际领先的自动化生产线5条，技术骨干20余人.自疫情发生以来，该企业积极响应政府号召，保障每天生产一次性无纺布健康防护口罩5万只左右.现从生产的大量口罩中抽取了100只作为样本，检测一项质量指标值，该项质量指标值落在区间[20,40）内的产品视为合格品，否则视为不合格品，如图是样本的频率分布直方图.
（1）求图中实数a的值；
（2）企业将不合格品全部销毁后，对合格品进行等级细分：质量指标值落在区间[25,30）内的定为一等品，每件售价2.4元；质量指标值落在区间[20,25）或[30,35）内的定为二等品，每件售价为1.8元；其他的合格品定为三等品，每件售价为1.2元.
用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.若有一名顾客随机购买2只口罩支付的费用为X（单位：元）.求X的分布列和数学期望.
【答案】（1）
；（2）分布列见解析，数学期望为
【解析】
（1）直接根据概率和为1计算得到答案.
（2）
的可能取值为
，计算概率得到分布列，再计算数学期望得到答案.
（1）
，解得.
（2）
，
，
.
故的可能取值为，
，
，
，
，
.
故分布列为：
|
|
|
|
|
|
|
|
|
|
|
|
故数学期望为：
.
【题目】某市四所重点中学进行高二期中联考，共有5000名学生参加，为了了解数学学科的学习情况，现从中随机地抽出若干名学生在这次测试中的数学成绩，制成如下频率分布表：
分组 | 频数 | 频率 |
| ① | ② |
| 0.050 | |
| 0.200 | |
| 36 | 0.300 |
| 0.275 | |
| 12 | ③ |
| 0.050 | |
合计 | ④ |
（1）根据上面的频率分布表，推出①②③④处的数字分别为 ， ， ， .
（2）补全
上的频率分布直方图.
（3）根据题中的信息估计总体：
①成绩在120分及以上的学生人数；
②成绩在
的频率.
【题目】某工厂的
,
,
三个不同车间生产同一产品的数量(单位:件)如下表所示.质检人员用分层抽样的方法从这些产品中共抽取6件样品进行检测:
车间 |
|
|
|
数量 | 50 | 150 | 100 |
(1)求这6件样品中来自,,各车间产品的数量;
(2)若在这6件样品中随机抽取2件进行进一步检测,求这2件产品来自相同车间的概率.
