Question

2．已知：方程$\sqrt{1-\frac{{x}^{2}}{4}}$=kx+2有两个不等实根，则k的取值范围为（　　）

• A． [-1，-$\frac{\sqrt{3}}{2}$）∪（$\frac{\sqrt{3}}{2}$，1]
• B． （-1，-$\frac{\sqrt{3}}{2}$）∪（$\frac{\sqrt{3}}{2}$，1）
• C． （-∞，-$\frac{\sqrt{3}}{2}$）∪（$\frac{\sqrt{3}}{2}$，+∞）
• D． （-$\frac{\sqrt{3}}{2}$，$\frac{\sqrt{3}}{2}$）

Answer 1

分析 设函数y=$\sqrt{1-\frac{{x}^{2}}{4}}$和y=kx+2，在坐标系中分别作出两个函数的图象，根据图象交点个数确定k的取值范围，

解答 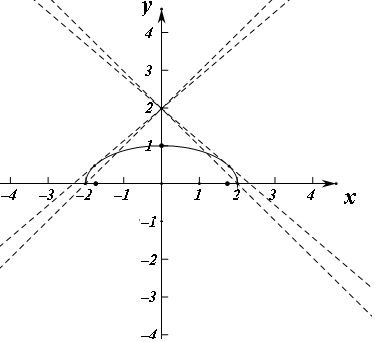解：设y=$\sqrt{1-\frac{{x}^{2}}{4}}$，y=kx+2，
在同一坐标系在图象如图：
当直线y=kx+2与椭圆的上半部分相切时即$\frac{{x}^{2}}{4}+（kx+2）^{2}=1$只有一个解时得到k=$±\frac{\sqrt{3}}{2}$，直线与椭圆的上半部分有两个交点时的斜率绝对值的最大值为$\frac{2-0}{2-0}$=1，
所以方程$\sqrt{1-\frac{{x}^{2}}{4}}$=kx+2有两个不等实根的k 的取值范围
[-1，-$\frac{\sqrt{3}}{2}$）∪（$\frac{\sqrt{3}}{2}$，1]；
故选A．

点评 本题主要考查方程根的个数的判断，利用方程和函数之间的关系，利用数形结合是解决此类问题的关键．