题目内容
设F1、F2分别为双曲线
-
=1(a>0,b>0)的左、右焦点,若在双曲线右支上存在点P,满足|PF1|-|PF2|=
|F1F2|,则该双曲线的渐近线方程为 .
| x2 |
| a2 |
| y2 |
| a2 |
| 3 |
| 5 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:利用双曲线的定义,结合条件,确定a,b,c的关系,即可求出双曲线的渐近线方程.
解答:
解:∵|PF1|-|PF2|=
|F1F2|,
∴2a=
•2c,
∴a=
c,
∴b=
a,
∴双曲线的渐近线方程为y=±
x,即y=±
x;
故答案为:y=±
x.
| 3 |
| 5 |
∴2a=
| 3 |
| 5 |
∴a=
| 3 |
| 5 |
∴b=
| 4 |
| 5 |
∴双曲线的渐近线方程为y=±
| b |
| a |
| 4 |
| 3 |
故答案为:y=±
| 4 |
| 3 |
点评:本题考查双曲线的渐近线方程,考查双曲线的定义,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
对于曲线y=ae
,令μ=lny,c=lna,v=
,可变换为线性回归模型,其形式为( )
| b |
| x |
| 1 |
| x |
| A、y=a+bv |
| B、μ=a+bv |
| C、μ=c+bv |
| D、y=c+bx |
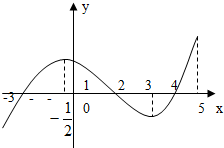 如果函数y=f(x)的导函数y=f′(x)的图象如图所示,给出下列判断:
如果函数y=f(x)的导函数y=f′(x)的图象如图所示,给出下列判断: