题目内容
已知三棱锥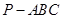 的底面
的底面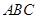 是直角三角形,且
是直角三角形,且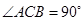 ,
,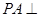 平面
平面 ,
,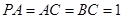 ,
,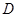 是线段
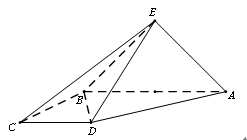
是线段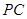 的中点,如图所示.
的中点,如图所示.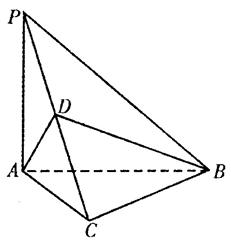
(Ⅰ)证明: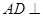 平面
平面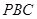 ;
;
(Ⅱ)求三棱锥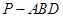 的体积.
的体积.
(1)证明线面垂直一般通过线线垂直来证明线面垂直,关键是对于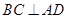 的证明。
的证明。
(2)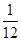
解析试题分析:(Ⅰ)证明:因为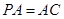 ,D是线段PC的中点,所以
,D是线段PC的中点,所以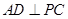 (1)
(1)
因为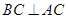 ,
,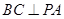 ,所以
,所以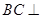 平面
平面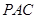 可得
可得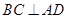 (2)
(2)
由(1)(2)得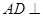 平面
平面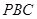 (6)
(6)
(Ⅱ)因为点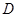 是线段
是线段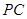 的中点,所以点
的中点,所以点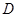 到平面
到平面 的距离等于点
的距离等于点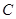 到平面
到平面 的距离的一半。因此
的距离的一半。因此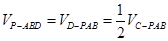 (9)
(9)
而 ,又
,又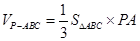 ,且
,且 ,
,
所以 即得
即得 即三棱锥
即三棱锥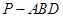 的体积为
的体积为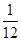 . 12分
. 12分
考点:空间中的垂直,体积
点评:解决关键是利用线面垂直的判定定理来证明垂直,同时利用的等体积法来求解 锥体的体积,属于基础题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
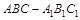 中,
中,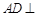 平面
平面 ,其垂足
,其垂足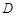 落在直线
落在直线 上.
上.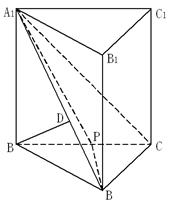
 ;
;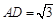 ,
,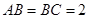 ,
,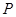 为
为 的中点,求三棱锥
的中点,求三棱锥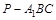 的体积.
的体积.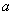 的正方形E, F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=
的正方形E, F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=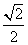 AD.
AD.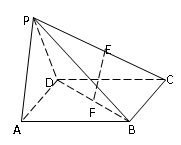
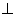 平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD
平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD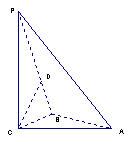
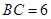 ,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.
,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.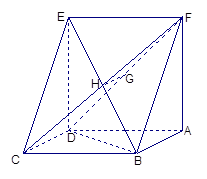
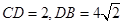 ,求四棱锥F-ABCD的体积.
,求四棱锥F-ABCD的体积.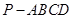 中,底面
中,底面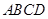 是矩形,侧棱
是矩形,侧棱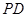 ⊥底面
⊥底面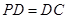 ,
, 是
是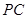 的中点,
的中点,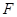 为
为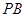 的中点.
的中点.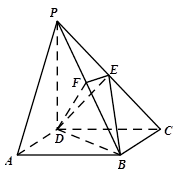
 平面
平面
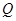 为直线
为直线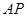 上任意一点,求几何体
上任意一点,求几何体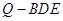 的体积;
的体积;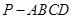 中,
中, ,
,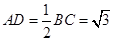 ,
,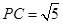 .
.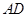 ∥
∥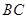 ,
,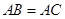 .
.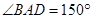
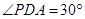 .
.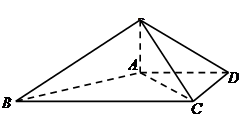
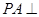 平面
平面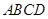 ;
;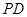 上是否存在一点
上是否存在一点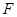 ,使直线
,使直线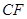 与平面
与平面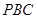 成角正弦值等于
成角正弦值等于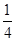 ,若存在,指出
,若存在,指出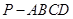 中,底面
中,底面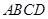 为矩
为矩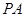 ⊥平面
⊥平面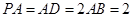 ,
,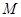 为
为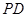 上的点,若
上的点,若
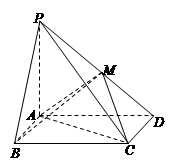
 的大小.
的大小. 与等腰直角三角形
与等腰直角三角形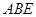 所在的平面互相垂直.
所在的平面互相垂直.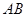 ∥
∥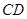 ,
,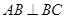 ,
, ,
, .
.
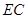 与平面
与平面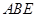 所成角的正弦值;
所成角的正弦值;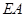 上是否存在点
上是否存在点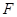 ,使
,使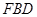 ?若存在,求出
?若存在,求出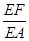 ;若不存在,说明理由.1
;若不存在,说明理由.1