题目内容
在直三棱柱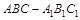 中,
中,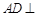 平面
平面 ,其垂足
,其垂足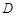 落在直线
落在直线 上.
上.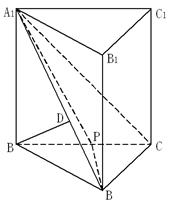
(1)求证: ;
;
(2)若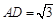 ,
,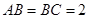 ,
,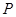 为
为 的中点,求三棱锥
的中点,求三棱锥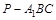 的体积.
的体积.
(1)证明如下 (2) 
解析试题分析:(Ⅰ)证明: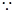 三棱柱
三棱柱 为直三棱柱,
为直三棱柱, 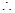
 平面
平面 ,
,
又 平面
平面 ,
, 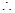

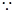
 平面
平面 ,且
,且 平面
平面 ,
, 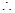
 .
.
又  平面
平面 ,
, 平面
平面 ,
, ,
, 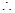
 平面
平面 ,又
,又 平面
平面 ,
, 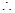

(2)在直三棱柱 中,
中,
 .
. 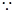
 平面
平面 ,其垂足
,其垂足 落在直线
落在直线 上,
上,
 .
.
在 中,
中,  ,
, ,
, ,
,
在 中,
中, 
由(1)知 平面
平面 ,
, 平面
平面 ,从而
,从而

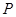 为
为 的中点,
的中点,


考点:直线与平面垂直的判定定理;几何体的体积公式
点评:在立体几何中,常考的定理是:直线与平面垂直的判定定理、直线与平面平行的判定定理。

练习册系列答案
相关题目
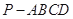 中,侧面
中,侧面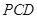
 底面
底面 ,
, ,底面
,底面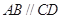 ,
,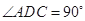 ,
,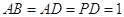 ,
,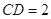 .
.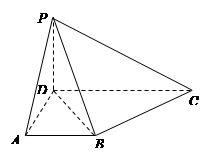
 平面
平面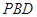 ;
; 为侧棱
为侧棱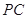 上一点,
上一点,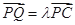 ,试确定
,试确定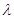 的值,使得二面角
的值,使得二面角 为
为 .
.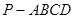 中,
中,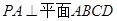 ,
,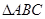 是正三角形,
是正三角形,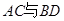 的交点
的交点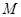 恰好是
恰好是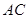 中点,又
中点,又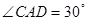 ,
,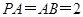 ,点
,点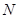 在线段
在线段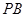 上,且
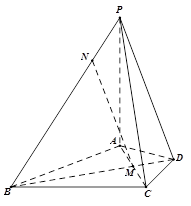
上,且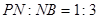 .
.
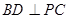 ;
;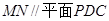 ;
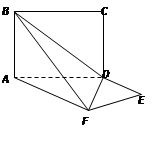
;
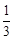 ,求AB的长.
,求AB的长. 中,
中,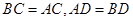 ,
,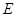 是
是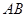 的中点.
的中点. 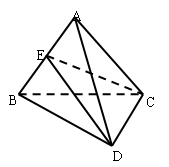
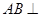 平面CDE;
平面CDE; 的重心,试在线段AE上确定一点F,使得GF//平面CDE.
的重心,试在线段AE上确定一点F,使得GF//平面CDE.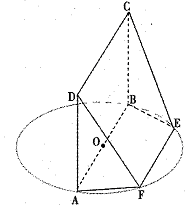
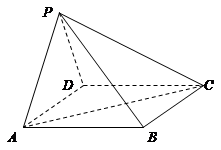
 ,其边长为2,
,其边长为2,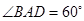 ,
,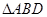 绕着
绕着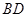 顺时针旋转
顺时针旋转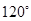 得到
得到 ,
,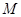 是
是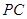 的中点.
的中点.
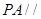 平面
平面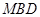 ;
;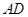 与平面
与平面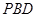 所成角的正弦值.
所成角的正弦值.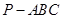 的底面
的底面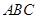 是直角三角形,且
是直角三角形,且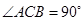 ,
,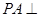 平面
平面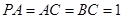 ,
,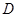 是线段
是线段 的中点,如图所示.
的中点,如图所示.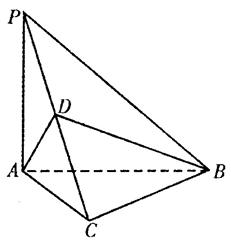
 平面
平面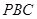 ;
;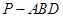 的体积.
的体积.