题目内容
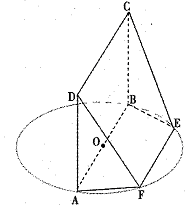
如图,在四棱锥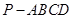 中,底面
中,底面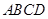 是矩形,侧棱
是矩形,侧棱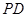 ⊥底面
⊥底面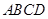 ,
,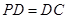 ,
, 是
是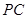 的中点,
的中点,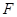 为
为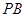 的中点.
的中点.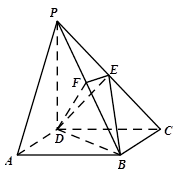
(1)证明: 平面
平面
(2)若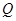 为直线
为直线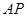 上任意一点,求几何体
上任意一点,求几何体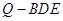 的体积;
的体积;
(1)要证明线面平行,则利用判定定理,先证明 ∥
∥ ,然后根据判定定理得到证明。
,然后根据判定定理得到证明。
(2)4
解析试题分析:
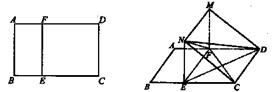
证明:(1)连结 交
交 与
与 ,连结
,连结 .
.
∵底面 是正方形,∴点
是正方形,∴点 是
是 的中点.
的中点.
又∵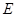 是
是 的中点∴在△
的中点∴在△ 中,
中, 为中位线 ∴
为中位线 ∴ ∥
∥ .
.
而
 平面
平面 ,
,
 平面
平面 ,∴
,∴ ∥平面
∥平面 .
.
(2) ∥平面
∥平面 ,
,
考点:线面平行,体积
点评:主要是考查了空间几何体的体积和线面平行的证明,属于基础题。

练习册系列答案
 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
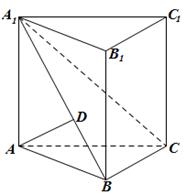
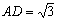 ,AB=BC=2,P为AC中点,求三棱锥
,AB=BC=2,P为AC中点,求三棱锥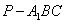 的体积。
的体积。 .
.
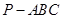 的底面
的底面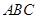 是直角三角形,且
是直角三角形,且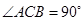 ,
,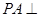 平面
平面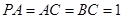 ,
,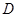 是线段
是线段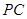 的中点,如图所示.
的中点,如图所示.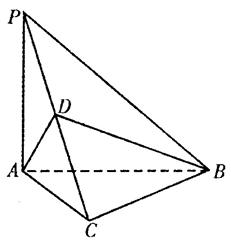
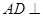 平面
平面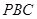 ;
;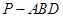 的体积.
的体积. 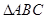 中,
中, 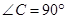 ,
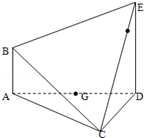
,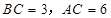 .D、E分别是
.D、E分别是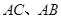 上的点,且
上的点,且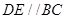 .将
.将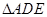 沿
沿 折起到
折起到 的位置,使
的位置,使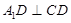 ,如图2.
,如图2.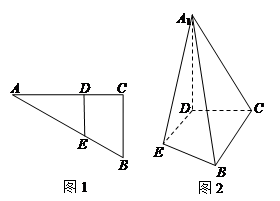
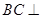 平面
平面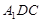 ;
;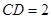 ,求
,求 与平面
与平面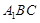 所成角的正弦值;
所成角的正弦值;