题目内容
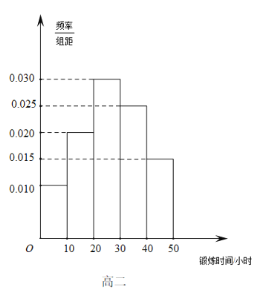
【题目】某中学调查防疫期间学生居家每天锻炼时间情况,从高一、高二年级学生中分别随机抽取100人,由调查结果得到如下的频率分布直方图:
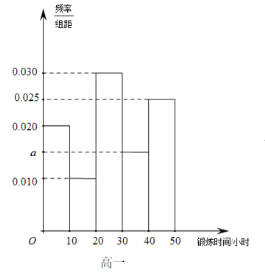
(Ⅰ)写出频率分布直方图(高一)中![]() 的值;记高一、高二学生100人锻炼时间的样本的方差分别为
的值;记高一、高二学生100人锻炼时间的样本的方差分别为![]() ,
,![]() ,试比较
,试比较![]() ,
,![]() 的大小(只要求写出结论);
的大小(只要求写出结论);
(Ⅱ)估计在高一、高二学生中各随机抽取1人,恰有一人的锻炼时间大于20分钟的概率;
(Ⅲ)由频率分布直方图可以认为,高二学生锻炼时间![]() 服从正态分布
服从正态分布![]() .其中
.其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差,且每名学生锻炼时间相互独立,设
近似为样本方差,且每名学生锻炼时间相互独立,设![]() 表示从高二学生中随机抽取10人,其锻炼时间位于
表示从高二学生中随机抽取10人,其锻炼时间位于![]() 的人数,求
的人数,求![]() 的数学期望.
的数学期望.
注:①同一组数据用该区间的中点值作代表,计算得![]()
②若![]() ,则
,则![]() ,
,![]()
【答案】(Ⅰ)![]() ,
,![]() ;(Ⅱ)0.42(Ⅲ)6.826
;(Ⅱ)0.42(Ⅲ)6.826
【解析】
(I)根据图中的数据即可判断方差的大小,利用频率总和为1即可求出![]() 的值;
的值;
(II)先设设事件![]() :在高一学生中随机抽取1人,其锻炼时间不大于20分钟,事件
:在高一学生中随机抽取1人,其锻炼时间不大于20分钟,事件![]() :在高二学生中随机抽取1人,其锻炼时间不大于20分钟,根据图形数据可得到它们的概率,而恰有一人的锻炼时间大于20分钟分两种情况:一种是这个人在高一;另一种是这个人在高二;再不出它们的概率和即可;
:在高二学生中随机抽取1人,其锻炼时间不大于20分钟,根据图形数据可得到它们的概率,而恰有一人的锻炼时间大于20分钟分两种情况:一种是这个人在高一;另一种是这个人在高二;再不出它们的概率和即可;
(III)利用所给的数据分别求出样本平均数![]() 和样本方差,代入公式即可求出概率和数学期望.
和样本方差,代入公式即可求出概率和数学期望.
解:(Ⅰ)![]() ,
,![]() ;
;
(Ⅱ)设事件![]() :在高一学生中随机抽取1人,其锻炼时间不大于20分钟,
:在高一学生中随机抽取1人,其锻炼时间不大于20分钟,
事件![]() :在高二学生中随机抽取1人,其锻炼时间不大于20分钟,
:在高二学生中随机抽取1人,其锻炼时间不大于20分钟,
事件![]() :在高一、高二学生中随机抽取1人,恰有一个学生锻炼时间大于20分钟,且另一个不大于20分钟,
:在高一、高二学生中随机抽取1人,恰有一个学生锻炼时间大于20分钟,且另一个不大于20分钟,
则![]() ,
,
![]() ,
,
![]() .
.
(Ⅲ)![]() ,由条件得
,由条件得![]() ,
,
从而![]() ,
,
![]() 从高二中随机抽取10人,其锻炼时间值位于
从高二中随机抽取10人,其锻炼时间值位于![]() 的概率是0.6826,
的概率是0.6826,
根据题意得![]() ,
,![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目