题目内容
已知f(x)=
(sinxcosx+cos2x-
),x∈[0,π],当方程f(x)=a有两个不相等的实根x1,x2时:
(1)当a的取值范围;
(2)求x1+x2的值.
| 2 |
| 1 |
| 2 |
(1)当a的取值范围;
(2)求x1+x2的值.
考点:二倍角的余弦
专题:三角函数的图像与性质
分析:(1)由二倍角的正弦、余弦公式,两角和的正弦公式化简解析式,由x得范围求出2x+
的范围,根据正弦函数的图象求出a的取值范围;
(2)根据图象可得(2x1+
)+(2x2+
)=π,化简求出x1+x2的值.
| π |
| 4 |
(2)根据图象可得(2x1+
| π |
| 4 |
| π |
| 4 |
解答:
解:(1)由题意得,f(x)=
(sinxcosx+cos2x-
)
=
(
sin2x+
-
)=
(
sin2x+
cos2x)
=sin(2x+
),
由x∈[0,π]得,2x+
∈[
,2π+
],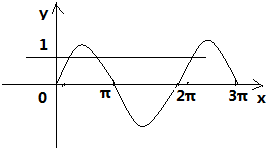
因为方程f(x)=a有两个不相等的实根x1,x2,
所以由正弦函数的图象可得,
<a<1,
则a的取值范围是(
,1);
(2)由图可得,(2x1+
)+(2x2+
)=π,
解得x1+x2=
.
| 2 |
| 1 |
| 2 |
=
| 2 |
| 1 |
| 2 |
| 1+cos2x |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=sin(2x+
| π |
| 4 |
由x∈[0,π]得,2x+
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |

因为方程f(x)=a有两个不相等的实根x1,x2,
所以由正弦函数的图象可得,
| ||
| 2 |
则a的取值范围是(
| ||
| 2 |
(2)由图可得,(2x1+
| π |
| 4 |
| π |
| 4 |
解得x1+x2=
| π |
| 4 |
点评:本题考查二倍角的正弦、余弦公式,两角和的正弦公式,方程的根转化为函数图象的交点问题,以及正弦函数的图象与性质,考查数形结合思想.

练习册系列答案
相关题目
 若函数f(x)=2sin(ωx+φ)的部分图象如图所示,为了得到这个函数的图象,只要将y=2sinx(x∈R)的图象上的所有的点( )
若函数f(x)=2sin(ωx+φ)的部分图象如图所示,为了得到这个函数的图象,只要将y=2sinx(x∈R)的图象上的所有的点( )A、纵坐标不变,横坐标缩短到原来的
| ||||
B、纵坐标不变,横坐标伸长到原来的2倍,再向左平移
| ||||
C、纵坐标不变,横坐标缩短到原来的
| ||||
D、纵坐标不变,横坐标伸长到原来的2倍,再向左平移
|