题目内容
(本小题满分14分)
已知动点M到点 的距离等于M到点
的距离等于M到点 的距离的
的距离的 倍.
倍.
(1)求动点M的轨迹C的方程;
(2)若直线 与轨迹C没有交点,求
与轨迹C没有交点,求 的取值范围;
的取值范围;
(3)已知圆 与轨迹C相交于
与轨迹C相交于 两点,求
两点,求
(1) 
(2)
(3)
【解析】
试题分析:注意把握求轨迹方程的四步曲,建系、设点、列式、化简,本题建系就省了,注意求哪个点的轨迹方程,就设哪个点的坐标为 ,根据题意,列出等量关系式,化简即可,对于第二问,注意考查的是圆与直线的位置关系,通过圆心到直线的距离与半径比较大小即可判断,对于第三问,涉及到两圆的公共弦长的问题,注意转化,将所求量放到相应的直角三角形中来求解.
,根据题意,列出等量关系式,化简即可,对于第二问,注意考查的是圆与直线的位置关系,通过圆心到直线的距离与半径比较大小即可判断,对于第三问,涉及到两圆的公共弦长的问题,注意转化,将所求量放到相应的直角三角形中来求解.
试题解析:
【解析】
(1)设 ,则
,则 , (2分)
, (2分)
整理得 ,即动点M的轨迹C的方程为
,即动点M的轨迹C的方程为 . (4分)
. (4分)
(2)由 ,消去
,消去 并化简得
并化简得 (6分)
(6分)
因为直线 与轨迹C没有交点,所以
与轨迹C没有交点,所以 (8分)
(8分)
即 ,解得
,解得 . (9分)
. (9分)
(3)圆 的圆心坐标为
的圆心坐标为 ,半径
,半径 (10分)
(10分)
由 得
得 这就是AB所在的直线方程, (11分)
这就是AB所在的直线方程, (11分)
又圆心 到直线AB的距离
到直线AB的距离 , (13分)
, (13分)
所以 . (14分)
. (14分)
或:AB所在的直线方程 与
与 的交点坐标为
的交点坐标为 , (13分)
, (13分)
所以
考点:求动点的轨迹方程,直线和圆的位置关系,两个圆的公共弦长问题.

练习册系列答案
相关题目
 B.
B.
 D.
D.
 满足
满足 ,则
,则
 C.1 D.
C.1 D.
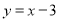 与抛物线
与抛物线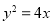 交于A、B两点,过A、B两点向抛物线的准线
交于A、B两点,过A、B两点向抛物线的准线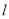 作垂线,垂足分别为P、Q,则梯形APQB的面积为
作垂线,垂足分别为P、Q,则梯形APQB的面积为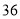 B.
B.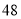 C.
C.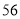 D.
D.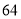
 的焦点坐标是
的焦点坐标是 B.
B.
 D.
D.

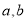 与平面
与平面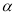 ,则下列四个命题中假命题是
,则下列四个命题中假命题是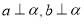 ,那么
,那么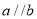 B.如果
B.如果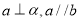 ,那么
,那么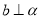
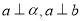 ,那么
,那么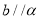 D.如果
D.如果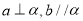 ,那么
,那么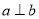
 与曲线
与曲线 有相同的( )
有相同的( ) 和分别以
和分别以 、
、 为直径的两个半圆组成,塑胶跑道宽8米(运动场平面图如图),已知塑胶跑道每平方米造价为150元,其它部分造价每平方米80元.
为直径的两个半圆组成,塑胶跑道宽8米(运动场平面图如图),已知塑胶跑道每平方米造价为150元,其它部分造价每平方米80元.
 (米),写出塑胶跑道面积
(米),写出塑胶跑道面积 与
与 的函数关系式
的函数关系式 ;
; 的范围为
的范围为 ,问当
,问当 取3近似计算).
取3近似计算).