题目内容
9.若两个等差数列{an},{bn}的前n项和分别为Sn,Tn,若对于任意的n∈N*,都有$\frac{{S}_{n}}{{T}_{n}}$=$\frac{2n-3}{4n-3}$,则$\frac{{a}_{9}}{{b}_{5}+{b}_{7}}$+$\frac{{a}_{3}}{{b}_{8}+{b}_{4}}$=$\frac{19}{41}$.分析 由等差数列的性质可得:$\frac{{a}_{9}}{{b}_{5}+{b}_{7}}$+$\frac{{a}_{3}}{{b}_{8}+{b}_{4}}$=$\frac{{a}_{9}}{2{b}_{6}}$+$\frac{{a}_{3}}{2{b}_{6}}$=$\frac{{a}_{6}}{{b}_{6}}$.又$\frac{{a}_{6}}{{b}_{6}}$=$\frac{\frac{11({a}_{1}+{a}_{11})}{2}}{\frac{11({b}_{1}+{b}_{11})}{2}}$=$\frac{{S}_{11}}{{T}_{11}}$,即可得出.
解答 解:由等差数列的性质可得:$\frac{{a}_{9}}{{b}_{5}+{b}_{7}}$+$\frac{{a}_{3}}{{b}_{8}+{b}_{4}}$=$\frac{{a}_{9}}{2{b}_{6}}$+$\frac{{a}_{3}}{2{b}_{6}}$=$\frac{{a}_{6}}{{b}_{6}}$.
∵对于任意的n∈N*,都有$\frac{{S}_{n}}{{T}_{n}}$=$\frac{2n-3}{4n-3}$,
∴$\frac{{a}_{6}}{{b}_{6}}$=$\frac{\frac{11({a}_{1}+{a}_{11})}{2}}{\frac{11({b}_{1}+{b}_{11})}{2}}$=$\frac{{S}_{11}}{{T}_{11}}$=$\frac{2×11-3}{4×11-3}$=$\frac{19}{41}$.
故答案为:$\frac{19}{41}$.
点评 本题考查了等差数列的通项公式及其前n项和公式性质,考查了推理能力与计算能力,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1 | B. | $\frac{{y}^{2}}{4}$-$\frac{{x}^{2}}{5}$=1 | C. | $\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{y}^{2}}{5}$-$\frac{{x}^{2}}{4}$=1 |

| A. | z>10? | B. | z≤10? | C. | z>20? | D. | z≤20? |
| A. | (-∞,2) | B. | [0,2) | C. | [2,+∞) | D. | (2,+∞) |
| A. | {-2,-1,1} | B. | {-1,1,2} | C. | {-1,1} | D. | {-2,-1} |
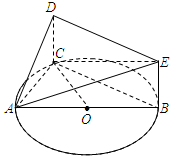 如图,AB是△ABC外接圆O的直径,四边形DCBE为矩形,且DC⊥平面ABC,AB=4,BE=1.
如图,AB是△ABC外接圆O的直径,四边形DCBE为矩形,且DC⊥平面ABC,AB=4,BE=1.