题目内容
已知α,β都是锐角,cosα•cosβ-sinα•sinβ=-
,cosα=
,求cosβ.
| 11 |
| 14 |
| 1 |
| 7 |
考点:两角和与差的余弦函数
专题:计算题,三角函数的求值
分析:利用同角三角函数间的关系可求得sin(α+β)与sinα的值,再利用两角差的余弦即可求得答案.
解答:
解:∵cosα•cosβ-sinα•sinβ=cos(α+β)=-
,α,β都是锐角,
∴sin(α+β)=
=
=
,
又cosα=
,
∴sinα=
,
∴cosβ=cos[(α+β)-α]
=cos(α+β)cosα+sin(α+β)sinα
=-
×
+
×
=
.
| 11 |
| 14 |
∴sin(α+β)=
| 1-cos2(α+β) |
1-(-
|
5
| ||
| 14 |
又cosα=
| 1 |
| 7 |
∴sinα=
4
| ||
| 7 |
∴cosβ=cos[(α+β)-α]
=cos(α+β)cosα+sin(α+β)sinα
=-
| 11 |
| 14 |
| 1 |
| 7 |
5
| ||
| 14 |
4
| ||
| 7 |
=
| 1 |
| 2 |
点评:本题考查同角三角函数间的关系,考查两角和与差的余弦函数,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
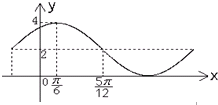 已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果
已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果