题目内容
已知函数f(x)＝Asin(ωx＋φ) 
的图象与y轴交于(0,3
)，它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(m,6)和
.
(1)求函数f(x)的解析式及m的值；
(2)若锐角θ满足tan θ＝2，求f(θ)．
解析：(1)由函数的图象在y轴右侧的第一个最高点和第一个最低点的坐标分别为(m,6)和，可得A＝6，
·T＝·
，求得ω＝2.
把点(0,3)代入函数的解析式可得
6sin(2×0＋φ)＝3，
解得sin φ＝
，再由|φ|＜
，求得φ＝
.
故f(x)＝6sin
.
函数在y轴右侧的第一个最高点的坐标分别为(m,6)，故2m＋＝
，解得m＝
.
(2)若锐角θ满足tan θ＝2，θ∈
，
∴sin θ＝
，cos θ＝
.
f(θ)＝6sin
＝6sin 2θ·cos＋6 cos 2θ·sin
＝6sin θcos θ＋3(2cos2θ－1)
练习册系列答案
相关题目
正数”的否定为( )
杆顶端的仰角分别为60°和30°，且第一排和最后一排的距离为10
m，则旗杆的高度为________m.
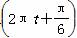，那么单摆来回摆动一次所需的时间为( )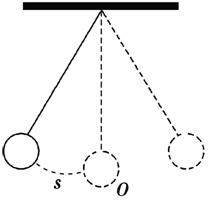
，θ∈
，则cos θ－sin θ＝________________.
对称
上是增函数
正周期为π
(sin2x－cos2x)－2sin xcos x.
，求f(x)的值域和单调递增区间．
，tan
＝
，则tan
的值是( )
B.
C.
D．－
点E，则线段DE的长为__________．