题目内容
已知函数 .(a∈R)
.(a∈R)(1)是否存在实数a使函数f(x)为奇函数?证明你的结论;
(2)用单调性定义证明:不论a取任何实数,函数f(x)在其定义域上都是增函数;
(3)若函数f(x)为奇函数,解不等式f(3m2-m+1)+f(2m-3)<0.
【答案】分析:(1)先求函数的定义域,然后利用奇函数的性质,可知f(0)=0可求a,即可
(2)先设x1<x2,然后判断f(x1)-f(x2)的正负,从而可判断f(x1)与f(x2)的大小,即可证明
(3)由已知可得f(3m2-m+1)<-f(2m-3),结合f(x)为奇函数及f(x)在R上是增函数可得3m2-m+1<3-2m,解不等式即可求解
解答:解:(1)∵3x>0
3x+1≠0函数f(x)的定义域为 R即(-∞,+∞)…(1分)
假设存在实数a使函数f(x)为奇函数,
由f(0)=0得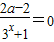 解得a=1…(2分),
解得a=1…(2分),
∴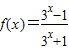
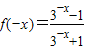 =
=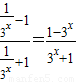 =
=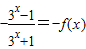
∴当a=1时,函数f(x)为奇函数…(4分)
(2)证明:任取x1,x2∈R,且x1<x2
∵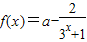
f(x1)-f(x2)=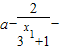
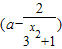
=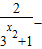
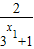
=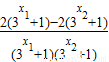
=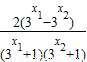 …(7分)
…(7分)
∵x1<x2,
∴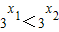
∴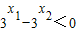
又∵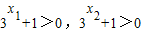
f(x1)-f(x2)<0即f(x1)<f(x2)
∴不论a取何值,函数f(x)在其定义域上都是增函数.…(9分)
(3)解:由f(3m2-m+1)+f(2m-3)<0得f(3m2-m+1)<-f(2m-3)
∵函数f(x)为奇函数
∴-f(2m-3)=f(3-2m)
∴f(3m2-m+1)<f(3-2m)
由(2)已证得函数f(x)在R上是增函数
∴f(3m2-m+1)<f(3-2m)?3m2-m+1<3-2m
∴3m2+m-2<0
∴(3m-2)(m+1)<0
∴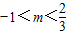 .
.
不等式f(3m2-m+1)+f(2m-3)<0的解集为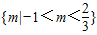 .…(14分)
.…(14分)
点评:本题主要考查了函数的奇偶性、函数的单调性的定义在证明函数的单调性的应用,抽象函数的单调性在求解不等式中的应用,属于函数知识的综合应用.
(2)先设x1<x2,然后判断f(x1)-f(x2)的正负,从而可判断f(x1)与f(x2)的大小,即可证明
(3)由已知可得f(3m2-m+1)<-f(2m-3),结合f(x)为奇函数及f(x)在R上是增函数可得3m2-m+1<3-2m,解不等式即可求解
解答:解:(1)∵3x>0
3x+1≠0函数f(x)的定义域为 R即(-∞,+∞)…(1分)
假设存在实数a使函数f(x)为奇函数,
由f(0)=0得
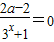 解得a=1…(2分),
解得a=1…(2分),∴
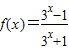
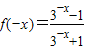 =
=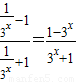 =
=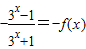
∴当a=1时,函数f(x)为奇函数…(4分)
(2)证明:任取x1,x2∈R,且x1<x2
∵
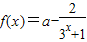
f(x1)-f(x2)=
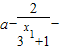
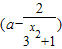
=
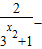
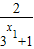
=
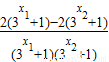
=
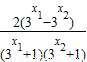 …(7分)
…(7分)∵x1<x2,
∴
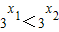
∴
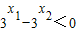
又∵
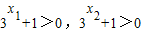
f(x1)-f(x2)<0即f(x1)<f(x2)
∴不论a取何值,函数f(x)在其定义域上都是增函数.…(9分)
(3)解:由f(3m2-m+1)+f(2m-3)<0得f(3m2-m+1)<-f(2m-3)
∵函数f(x)为奇函数
∴-f(2m-3)=f(3-2m)
∴f(3m2-m+1)<f(3-2m)
由(2)已证得函数f(x)在R上是增函数
∴f(3m2-m+1)<f(3-2m)?3m2-m+1<3-2m
∴3m2+m-2<0
∴(3m-2)(m+1)<0
∴
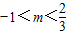 .
.不等式f(3m2-m+1)+f(2m-3)<0的解集为
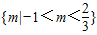 .…(14分)
.…(14分)点评:本题主要考查了函数的奇偶性、函数的单调性的定义在证明函数的单调性的应用,抽象函数的单调性在求解不等式中的应用,属于函数知识的综合应用.

练习册系列答案
相关题目
 ,其中a∈R.
,其中a∈R.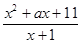 (a∈R),若对于任意的X∈N*,f(x)≥3恒成立,则a的取值范围是___
(a∈R),若对于任意的X∈N*,f(x)≥3恒成立,则a的取值范围是___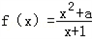 (其中a∈R).
(其中a∈R).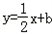 ,求实数a,b的值;
,求实数a,b的值;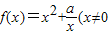 ,常数a∈R),若函数f(x)在x∈[2,+∞)上是增函数,则a的取值范围是 .
,常数a∈R),若函数f(x)在x∈[2,+∞)上是增函数,则a的取值范围是 .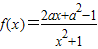 ,其中a∈R.
,其中a∈R.