题目内容
已知函数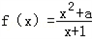 (其中a∈R).
(其中a∈R).
(Ⅰ)若函数f(x)在点(1,f(1))处的切线为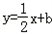 ,求实数a,b的值;
,求实数a,b的值;
(Ⅱ)求函数f(x)的单调区间.
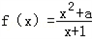 (其中a∈R).
(其中a∈R).(Ⅰ)若函数f(x)在点(1,f(1))处的切线为
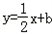 ,求实数a,b的值;
,求实数a,b的值;(Ⅱ)求函数f(x)的单调区间.
解:由 ,可得
,可得 .
.
(Ⅰ)因为函数f(x)在点(1,f(1))处的切线为 ,得:
,得:
解得
(Ⅱ)令f'(x)>0,得x2+2x﹣a>0…①
当△=4+4a≤0,即a≤﹣1时,不等式①在定义域内恒成立,
所以此时函数f(x)的单调递增区间为(﹣∞,﹣1)和(﹣1,+∞).
当△=4+4a>0,即a>﹣1时,不等式①的解为 或
或 ,
,
又因为x≠﹣1,所以此时函数f(x)的单调递增区间为 和
和 ,单调递减区间为
,单调递减区间为 和
和
所以,当a≤﹣1时,函数f(x)的单调递增区间为(﹣∞,﹣1)和(﹣1,+∞);
当a>﹣1时,函数f(x)的单调递增区间为 和
和 ,单调递减区间为
,单调递减区间为 和
和 ..
..
 ,可得
,可得 .
.(Ⅰ)因为函数f(x)在点(1,f(1))处的切线为
 ,得:
,得:
解得

(Ⅱ)令f'(x)>0,得x2+2x﹣a>0…①
当△=4+4a≤0,即a≤﹣1时,不等式①在定义域内恒成立,
所以此时函数f(x)的单调递增区间为(﹣∞,﹣1)和(﹣1,+∞).
当△=4+4a>0,即a>﹣1时,不等式①的解为
 或
或 ,
,又因为x≠﹣1,所以此时函数f(x)的单调递增区间为
 和
和 ,单调递减区间为
,单调递减区间为 和
和
所以,当a≤﹣1时,函数f(x)的单调递增区间为(﹣∞,﹣1)和(﹣1,+∞);
当a>﹣1时,函数f(x)的单调递增区间为
 和
和 ,单调递减区间为
,单调递减区间为 和
和 ..
..
练习册系列答案
相关题目
 ,其中a∈R.
,其中a∈R. ,其中a∈R.
,其中a∈R. ,其中a∈R.
,其中a∈R.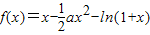 ,其中a∈R.
,其中a∈R. ,其中a∈R.
,其中a∈R.