题目内容
已知函数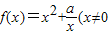
，常数a∈R），若函数f（x）在x∈[2，+∞）上是增函数，则a的取值范围是 ．
【答案】分析：求出函数的导数，利用其在[2，+∞）上是增函数，建立不等式，求出参数a的取值范围．
解答：解：由题设，f'（x）=2x-
又函数f（x）在x∈[2，+∞）上是增函数
∴f'（x）=2x-
≥0在[2，+∞）上恒成立，
即a≤2x3在[2，+∞）上恒成立，
因为2x3≥16，故a≤16
故应填a≤16
点评：考查求导公式，以及函数在某个区间上是增函数转化为其导数在该区间上大于等于0恒成立这一结论．
解答：解：由题设，f'（x）=2x-
又函数f（x）在x∈[2，+∞）上是增函数
∴f'（x）=2x-
≥0在[2，+∞）上恒成立，即a≤2x3在[2，+∞）上恒成立，
因为2x3≥16，故a≤16
故应填a≤16
点评：考查求导公式，以及函数在某个区间上是增函数转化为其导数在该区间上大于等于0恒成立这一结论．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
，常数a∈R）．
，常数a∈R），若函数f（x）在x∈[2，+∞）上是增函数，则a的取值范围是 ．
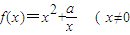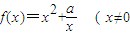，常数a∈R）．
，常数a∈R）．
，常数a∈R）．