题目内容
已知函数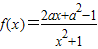 ,其中a∈R.
,其中a∈R.(Ⅰ)当a=1时,求曲线y=f(x)在原点处的切线方程;
(Ⅱ)求f(x)的单调区间;
(Ⅲ)若f(x)在[0,+∞)上存在最大值和最小值,求a的取值范围.
【答案】分析:(Ⅰ)当a=1时,先对函数求导,然后求出 f'(0),即取消在原点处的切线斜率,可求得曲线y=f(x)在原点处的切线方程
(Ⅱ)先对函数求导,然后根据导数的符号可判断函数的单调区间
(III)由(Ⅱ)中函数的单调区间,可求出函数的最值取得的条件,然后可求a的范围
解答:(Ⅰ)解:当a=1时, ,
, . …(2分)
. …(2分)
由 f'(0)=2,得曲线y=f(x)在原点处的切线方程是2x-y=0.…(3分)
(Ⅱ)解:对函数求导可得, …(4分)
…(4分)
①当a=0时, .
.
所以f(x)在(0,+∞)单调递增,在(-∞,0)单调递减. …(5分)
当a≠0, .
.
②当a>0时,令f'(x)=0,得x1=-a, ,f(x)与f'(x)的情况如下:
,f(x)与f'(x)的情况如下:
故f(x)的单调减区间是(-∞,-a), ;单调增区间是
;单调增区间是 . …(7分)
. …(7分)
③当a<0时,f(x)与f'(x)的情况如下:
所以f(x)的单调增区间是 ;单调减区间是
;单调减区间是 ,(-a,+∞).…(9分)
,(-a,+∞).…(9分)
(Ⅲ)解:由(Ⅱ)得,a=0时不合题意. …(10分)
当a>0时,由(Ⅱ)得,f(x)在 单调递增,在
单调递增,在 单调递减,
单调递减,
所以f(x)在(0,+∞)上存在最大值 .
.
设x为f(x)的零点,易知 ,且
,且 .从而x>x时,f(x)>0;x<x时,f(x)<0.
.从而x>x时,f(x)>0;x<x时,f(x)<0.
若f(x)在[0,+∞)上存在最小值,必有f(0)≤0,解得-1≤a≤1.
所以a>0时,若f(x)在[0,+∞)上存在最大值和最小值,a的取值范围是(0,1].…(12分)
当a<0时,由(Ⅱ)得,f(x)在(0,-a)单调递减,在(-a,+∞)单调递增,
所以f(x)在(0,+∞)上存在最小值f(-a)=-1.
若f(x)在[0,+∞)上存在最大值,必有f(0)≥0,解得a≥1,或a≤-1.
所以a<0时,若f(x)在[0,+∞)上存在最大值和最小值,a的取值范围是(-∞,-1].
综上,a的取值范围是(-∞,-1]∪(0,1]. …(14分)
点评:本题主要考查了函数的导数的几何意义的应用,导数在函数的单调区间及函数的最值求解中的应用,属于中档试题
(Ⅱ)先对函数求导,然后根据导数的符号可判断函数的单调区间
(III)由(Ⅱ)中函数的单调区间,可求出函数的最值取得的条件,然后可求a的范围
解答:(Ⅰ)解:当a=1时,
 ,
, . …(2分)
. …(2分)由 f'(0)=2,得曲线y=f(x)在原点处的切线方程是2x-y=0.…(3分)
(Ⅱ)解:对函数求导可得,
 …(4分)
…(4分)①当a=0时,
 .
.所以f(x)在(0,+∞)单调递增,在(-∞,0)单调递减. …(5分)
当a≠0,
 .
.②当a>0时,令f'(x)=0,得x1=-a,
 ,f(x)与f'(x)的情况如下:
,f(x)与f'(x)的情况如下:| x | (-∞,x1) | x1 | (x1,x2) | x2 | (x2,+∞) |
| f'(x) | - | + | - | ||
| f(x) | ↘ | f(x1) | ↗ | f(x2) | ↘ |
 ;单调增区间是
;单调增区间是 . …(7分)
. …(7分)③当a<0时,f(x)与f'(x)的情况如下:
| x | (-∞,x2) | x2 | (x2,x1) | x1 | (x1,+∞) |
| f'(x) | + | - | + | ||
| f(x) | ↗ | f(x2) | ↘ | f(x1) | ↗ |
 ;单调减区间是
;单调减区间是 ,(-a,+∞).…(9分)
,(-a,+∞).…(9分)(Ⅲ)解:由(Ⅱ)得,a=0时不合题意. …(10分)
当a>0时,由(Ⅱ)得,f(x)在
 单调递增,在
单调递增,在 单调递减,
单调递减,所以f(x)在(0,+∞)上存在最大值
 .
.设x为f(x)的零点,易知
 ,且
,且 .从而x>x时,f(x)>0;x<x时,f(x)<0.
.从而x>x时,f(x)>0;x<x时,f(x)<0.若f(x)在[0,+∞)上存在最小值,必有f(0)≤0,解得-1≤a≤1.
所以a>0时,若f(x)在[0,+∞)上存在最大值和最小值,a的取值范围是(0,1].…(12分)
当a<0时,由(Ⅱ)得,f(x)在(0,-a)单调递减,在(-a,+∞)单调递增,
所以f(x)在(0,+∞)上存在最小值f(-a)=-1.
若f(x)在[0,+∞)上存在最大值,必有f(0)≥0,解得a≥1,或a≤-1.
所以a<0时,若f(x)在[0,+∞)上存在最大值和最小值,a的取值范围是(-∞,-1].
综上,a的取值范围是(-∞,-1]∪(0,1]. …(14分)
点评:本题主要考查了函数的导数的几何意义的应用,导数在函数的单调区间及函数的最值求解中的应用,属于中档试题

练习册系列答案
相关题目
 ,其中a∈R.
,其中a∈R. ,其中a∈R.
,其中a∈R. ,其中a∈R.
,其中a∈R.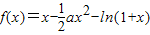 ,其中a∈R.
,其中a∈R. ,其中a∈R.
,其中a∈R.