题目内容
如图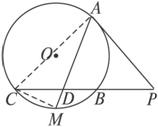
图
思路分析:由PB·PC=PA2,联想到证PA=PD.
证明:连结AC、MC.
∵PA是切线,AM是弦,∴∠PAD=∠ACM.
∵∠ADP=∠ACD+∠CAD, ![]() ,
,
∴∠CAM=∠MCB.
∴∠ADP=∠ACD+∠MCD=∠ACM.
∴∠ADP=∠PAD.∴PA=PD.
又由切割线定理,得PA2=PB·PC,
∴PD2=PB·PC.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
题目内容
如图
图
思路分析:由PB·PC=PA2,联想到证PA=PD.
证明:连结AC、MC.
∵PA是切线,AM是弦,∴∠PAD=∠ACM.
∵∠ADP=∠ACD+∠CAD, ![]() ,
,
∴∠CAM=∠MCB.
∴∠ADP=∠ACD+∠MCD=∠ACM.
∴∠ADP=∠PAD.∴PA=PD.
又由切割线定理,得PA2=PB·PC,
∴PD2=PB·PC.

 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案