题目内容
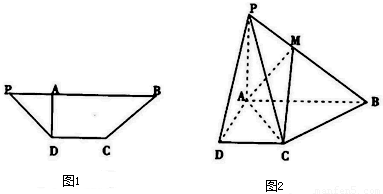
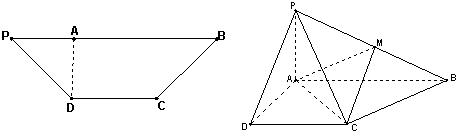
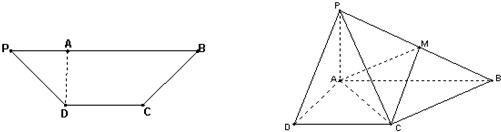
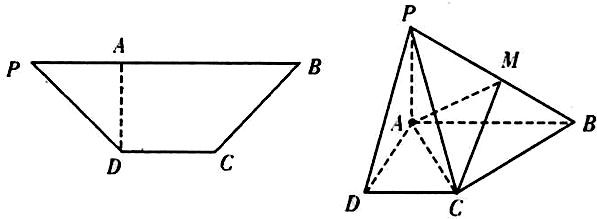
在等腰梯形PDCB(图1)中,DC∥PB,PB=3DC=3,PD=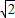 ,DA⊥PB,垂足为A,将△PAD沿AD折起,使得PA⊥AB,得到四棱锥P-ABCD(图2).在图2中完成下面问题:
,DA⊥PB,垂足为A,将△PAD沿AD折起,使得PA⊥AB,得到四棱锥P-ABCD(图2).在图2中完成下面问题:(1)证明:平面PAD⊥平面PCD;
(2)点M在棱PB上,平面AMC把四棱锥P-ABCD分成两个几何体(如图2),当这两个几何体的体积之比VPM-ACDVM-ABC=5:4时,求
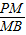 的值;
的值;(3)在(2)的条件下,证明:PD‖平面AMC.
【答案】分析:(1)由图1中DA⊥PB,可得折叠后DA⊥AB,DA⊥PA,进而DC⊥PA,DC⊥DA,由线面垂直的判定定理得到DC⊥平面PAD,再由面面垂直的判定定理得到平面PAD⊥平面PCD;
(2)设MN=h,则可得VM-ABC=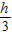 ,VP-ABCD=
,VP-ABCD= ,则VPM-ABCD=VP-ABCD-VM-ABC=
,则VPM-ABCD=VP-ABCD-VM-ABC= -
-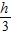 ,结合VPM-ABCD:VM-ABC=5:4,可求出h值,进而得到
,结合VPM-ABCD:VM-ABC=5:4,可求出h值,进而得到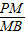 的值;
的值;
(3)在梯形ABCD中,连接AC、BD交于点O,连接OM.易知△AOB∽△DOC,所以在平面PBD中,有PD∥MO,进而由线面平行的判定定理得到答案.
解答:证明:(1)因为在图a的等腰梯形PDCB中,DA⊥PB,
所以在四棱锥P-ABCD中,DA⊥AB,DA⊥PA.…(1分)
又PA⊥AB,且DC∥AB,所以DC⊥PA,DC⊥DA,…(2分)
而DA?平面PAD,PA?平面PAD,PA∩DA=A,
所以DC⊥平面PAD.…(3分)
因为DC?平面PCD,
所以平面PAD⊥平面PCD.…(4分)
解:(2)因为DA⊥PA,且PA⊥AB
所以PA⊥平面ABCD,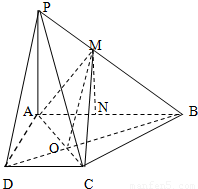
又PA?平面PAB,
所以平面PAB⊥平面ABC.
如图,过M作MN⊥AB,垂足为N,
则MN⊥平面ABCD.…(5分)
在等腰梯形PDCB中,DC∥PB,
PB=3DC=3,PD=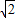 ,DA⊥PB,
,DA⊥PB,
所以PA=1,AB=2,AD=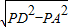 =1.…(6分)
=1.…(6分)
设MN=h,则VM-ABC= S△ABC•h=
S△ABC•h=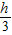 .…(7分)
.…(7分)
VP-ABCD= S梯形ABCD•PA=
S梯形ABCD•PA=
VPM-ABCD=VP-ABCD-VM-ABC= -
- .…(8分)
.…(8分)
因为VPM-ABCD:VM-ABC=5:4,
所以( -
-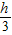 ):
):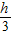 =5:4,解得h=
=5:4,解得h= .…(9分)
.…(9分)
在△PAB中,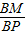 =
=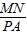 =
= ,所以BM=
,所以BM= BP,MP=
BP,MP= BP.
BP.
所以PM:MB=1:2.…(10分)
(3)在梯形ABCD中,连接AC、BD交于点O,连接OM.
易知△AOB∽△DOC,所以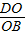 =
=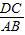 =
= .…(11分)
.…(11分)
又PM:MB=1:2,所以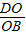 =
=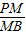 ,…(12分)
,…(12分)
所以在平面PBD中,有PD∥MO.…(13分)
又因为PD?平面AMC,MO?平面AMC,
所以PD∥平面AMC.…(14分)
点评:本题考查的知识点是平面与平面垂直的判定,直线与平面平行的判定,棱锥的体积,熟练掌握空间线面关系的判定定理,性质定理及几何特征是解答本题的关键.
(2)设MN=h,则可得VM-ABC=
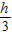 ,VP-ABCD=
,VP-ABCD= ,则VPM-ABCD=VP-ABCD-VM-ABC=
,则VPM-ABCD=VP-ABCD-VM-ABC= -
-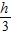 ,结合VPM-ABCD:VM-ABC=5:4,可求出h值,进而得到
,结合VPM-ABCD:VM-ABC=5:4,可求出h值,进而得到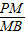 的值;
的值;(3)在梯形ABCD中,连接AC、BD交于点O,连接OM.易知△AOB∽△DOC,所以在平面PBD中,有PD∥MO,进而由线面平行的判定定理得到答案.
解答:证明:(1)因为在图a的等腰梯形PDCB中,DA⊥PB,
所以在四棱锥P-ABCD中,DA⊥AB,DA⊥PA.…(1分)
又PA⊥AB,且DC∥AB,所以DC⊥PA,DC⊥DA,…(2分)
而DA?平面PAD,PA?平面PAD,PA∩DA=A,
所以DC⊥平面PAD.…(3分)
因为DC?平面PCD,
所以平面PAD⊥平面PCD.…(4分)
解:(2)因为DA⊥PA,且PA⊥AB
所以PA⊥平面ABCD,

又PA?平面PAB,
所以平面PAB⊥平面ABC.
如图,过M作MN⊥AB,垂足为N,
则MN⊥平面ABCD.…(5分)
在等腰梯形PDCB中,DC∥PB,
PB=3DC=3,PD=
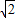 ,DA⊥PB,
,DA⊥PB,所以PA=1,AB=2,AD=
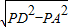 =1.…(6分)
=1.…(6分)设MN=h,则VM-ABC=
 S△ABC•h=
S△ABC•h=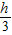 .…(7分)
.…(7分)VP-ABCD=
 S梯形ABCD•PA=
S梯形ABCD•PA=
VPM-ABCD=VP-ABCD-VM-ABC=
 -
- .…(8分)
.…(8分)因为VPM-ABCD:VM-ABC=5:4,
所以(
 -
-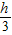 ):
):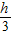 =5:4,解得h=
=5:4,解得h= .…(9分)
.…(9分)在△PAB中,
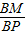 =
=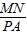 =
= ,所以BM=
,所以BM= BP,MP=
BP,MP= BP.
BP.所以PM:MB=1:2.…(10分)
(3)在梯形ABCD中,连接AC、BD交于点O,连接OM.
易知△AOB∽△DOC,所以
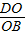 =
=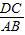 =
= .…(11分)
.…(11分)又PM:MB=1:2,所以
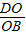 =
=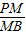 ,…(12分)
,…(12分)所以在平面PBD中,有PD∥MO.…(13分)
又因为PD?平面AMC,MO?平面AMC,
所以PD∥平面AMC.…(14分)
点评:本题考查的知识点是平面与平面垂直的判定,直线与平面平行的判定,棱锥的体积,熟练掌握空间线面关系的判定定理,性质定理及几何特征是解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
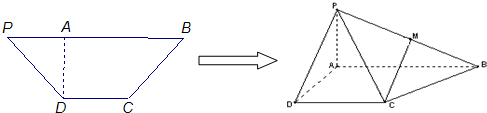
 (2013•广州三模)如图,在等腰梯形PDCB中,PB∥CD,PB=3,DC=1,PD=BC=
(2013•广州三模)如图,在等腰梯形PDCB中,PB∥CD,PB=3,DC=1,PD=BC=