题目内容
已知向量 ,
, ,函数
,函数 ,
, 三个内角
三个内角 的对边分别为
的对边分别为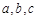 .
.
(1)求 的单调递增区间;
的单调递增区间;
(2)若
 ,求
,求 的面积
的面积 .
.
(1)函数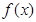 的单调增区间为
的单调增区间为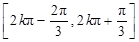
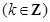 .
.
(2) 的面积
的面积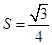 .
.
解析试题分析:(1)根据平面向量的数量积,应用和差倍半的三角函数公式,将 化简为
化简为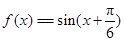 ,讨论函数的单调性;
,讨论函数的单调性;
(2) 本题解答可有两种思路,在利用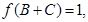 得到
得到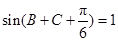 ,
,
求得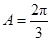 后,一是可应用正弦定理
后,一是可应用正弦定理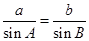 ,得到
,得到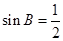 ,
,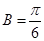 或者
或者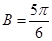 根据
根据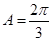 为钝角,确定
为钝角,确定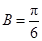 ,得
,得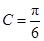 ;二是应用余弦定理,
;二是应用余弦定理, ,得
,得 ,
,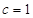 或
或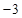 (舍去),进一步确定
(舍去),进一步确定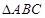 的面积
的面积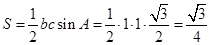 .
.
试题解析:(1)由题意得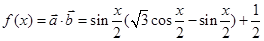
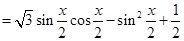
=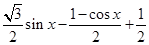 =
=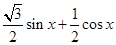
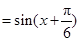 , 3分
, 3分
令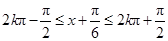

解得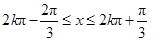

所以函数 的单调增区间为
的单调增区间为
 . 6分
. 6分
(2) 解法一:因为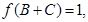 所以
所以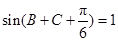 ,
,
又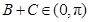 ,
,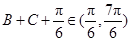 ,
,
所以 ,所以
,所以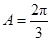 , 8分
, 8分
由正弦定理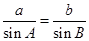 把
把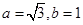 代入,得到
代入,得到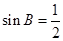 10分
10分
得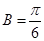 或者
或者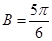 ,因为
,因为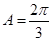 为钝角,所以
为钝角,所以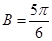 舍去
舍去
所以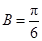 ,得
,得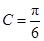 .
.
所以,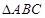 的面积
的面积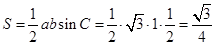 . 12分
. 12分
解法二:同上(略)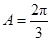 , 8分
, 8分
由余弦定理, ,得
,得 ,
,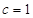 或
或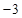 (舍去)10分
(舍去)10分
所以,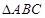 的面积
的面积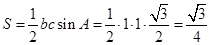 . 12分
. 12分
考点:平面向量的数量积,和差倍半的三角函数,正弦定理、余弦定理的应用,三角形面积公式.

练习册系列答案
相关题目
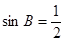 .
.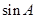 和
和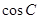 的值;
的值;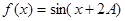 ,求
,求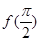 的值.
的值.
 ,求
,求 的值.
的值.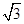 sin x,1),n=(cos x,-y),且m⊥n.
sin x,1),n=(cos x,-y),且m⊥n. =3,且a=2,b+c=4,求△ABC的面积.
=3,且a=2,b+c=4,求△ABC的面积. (其中C为锐角).
(其中C为锐角).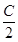 +ccos2
+ccos2 =
= b.
b. 中,角
中,角 、
、 、
、 对的边分别为
对的边分别为 、
、 、
、 ,且
,且
 的值;
的值; ,求
,求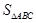 .
. ),n=
),n= ,且m∥n
,且m∥n