题目内容
在 中,角
中,角 、
、 、
、 对的边分别为
对的边分别为 、
、 、
、 ,且
,且
(1)求 的值;
的值;
(2)若 ,求
,求 的面积
的面积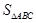 .
.
(1)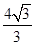 (2);
(2);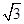
解析试题分析:(1)首先根据正弦定理,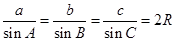 ,利用条件中
,利用条件中 的值求出
的值求出 的值.
的值.
而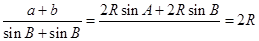 ,问题得解.
,问题得解.
(2)由于已知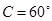 ,根据三角形的面积公式:
,根据三角形的面积公式: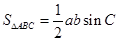 ,只需再求出
,只需再求出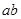 的值.
的值.
由余弦定理,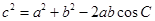 得:
得: ,结合条件
,结合条件
可解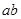 ,并进而求出
,并进而求出 的面积.
的面积.
试题解析:(1)由正弦定理可得: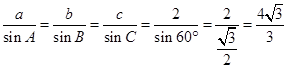 ,
,
所以  ,
,
所以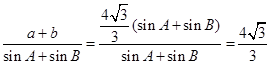 6分
6分
(2)由余弦定理得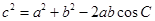 ,即
,即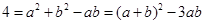 ,
,
又 ,所以
,所以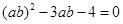 ,解得
,解得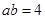 或
或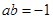 (舍去),
(舍去),
所以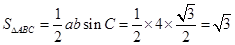 12分
12分
考点:1、正弦定理;2、余弦定理;3、三角形的面积公式.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
 ,
, ,函数
,函数 ,
, 三个内角
三个内角 的对边分别为
的对边分别为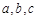 .
. 的单调递增区间;
的单调递增区间;
 ,求
,求 的面积
的面积 .
. ,求a的值.
,求a的值. sin xcos x+cos 2x-
sin xcos x+cos 2x- ,△ABC三个内角A,B,C的对边分别为a,b,c,且f(B)=1.
,△ABC三个内角A,B,C的对边分别为a,b,c,且f(B)=1. 中,
中, 分别是角A,B,C的对边,且满足
分别是角A,B,C的对边,且满足 .
. ,且
,且 ,求最小边长.
,求最小边长. 为
为 ,
, 的等差中项.
的等差中项. 中,角
中,角 ,
, ,
, 所对的边分别是
所对的边分别是 ,
, ,
, ,已知
,已知 ,
, .
. ,求
,求 ,求
,求