题目内容
在DABC中,角A、B、C的对边分别为a、b、c,且角A、B都是锐角,a=6,b=5,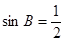 .
.
(1) 求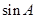 和
和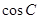 的值;
的值;
(2) 设函数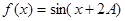 ,求
,求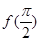 的值.
的值.
(1) (2)
(2)
解析试题分析:
(1)在三角形ABC中,可以利用A,B角的正弦定理把A角的正弦值求出来,因为A,B角都是锐角,所以利用正余弦之间的关系可以求出A,B角的余弦值,再根据三角形的三个内角和为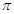 ,可得
,可得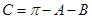 ,则利用诱导公式和余弦的和差角公式即可利用A,B角的正余弦值来表示角C的余弦值.进而求的角c的余弦值.
,则利用诱导公式和余弦的和差角公式即可利用A,B角的正余弦值来表示角C的余弦值.进而求的角c的余弦值.
(2)把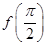 带入函数
带入函数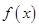 的解析式,利用诱导公式(奇变偶不变,符号看象限)可得
的解析式,利用诱导公式(奇变偶不变,符号看象限)可得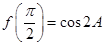 ,利用余弦值的二倍角公式可以利用角A的正弦值或者余弦值来求的
,利用余弦值的二倍角公式可以利用角A的正弦值或者余弦值来求的 ,进而得到
,进而得到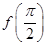 的值.
的值.
试题解析:
(1)由正弦定理 ,得
,得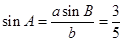 . (3分)
. (3分)
∵A、B是锐角,∴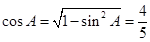 , (4分)
, (4分)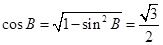 , (5分)
, (5分)
由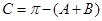 ,得
,得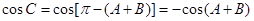 (6分)
(6分) (7分)
(7分) (8分)
(8分)
(2)由(1)知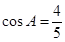 ,
,
∴ (11分)
(11分)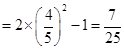 (12分)
(12分)
考点:正余弦值的关系 正余弦值的和差角公式 诱导公式 余弦倍角公式

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
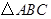 中,角A,B,C的对边分别为a,b,c,已知
中,角A,B,C的对边分别为a,b,c,已知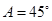 ,
, .
.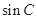 的值;
的值;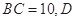 为
为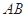 的中点,求
的中点,求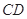 的长.
的长.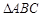 中,已知
中,已知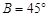 ,
,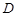 是
是 边上的一点,
边上的一点,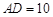 ,
,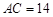 ,
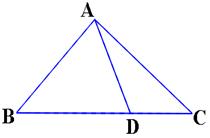
,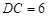 .
.
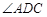 的大小;
的大小;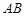 的长.
的长.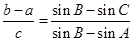 ,关于x的不等式x2cosC+4xsinC+6≥0对任意的x∈R恒成立.
,关于x的不等式x2cosC+4xsinC+6≥0对任意的x∈R恒成立. .
. ,求
,求 的取值范围;
的取值范围; 的内角A、B、C所对的边分别为a、b、c,已知
的内角A、B、C所对的边分别为a、b、c,已知 为锐角,
为锐角, ,
, ,
, ,求
,求 的值.
的值. 中,角
中,角 所对的边分别为
所对的边分别为 ,已知
,已知 ,
, ,
, ,求
,求 .
. ,
, ,函数
,函数 ,
, 三个内角
三个内角 的对边分别为
的对边分别为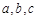 .
. 的单调递增区间;
的单调递增区间;
 ,求
,求 的面积
的面积 .
. ),且m⊥n.
),且m⊥n.