题目内容
2.如图是函数f(x)=-x2+ax+b的部分图象,f′(x)是f(x)的导函数,则函数g(x)=ex-f′(x)的零点所在的区间是( )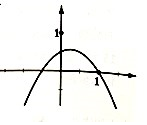
| A. | (-1,-$\frac{1}{2}$) | B. | (-$\frac{1}{2}$,0) | C. | (0,$\frac{1}{2}$) | D. | ($\frac{1}{2}$,1) |
分析 由二次函数图象的对称轴确定a的范围,据g(x)的表达式计算g(0)和g($\frac{1}{2}$)的值的符号,从而确定零点所在的区间.
解答 解:∵二次函数f(x)图象的对称轴 x=$\frac{a}{2}$∈( $\frac{1}{2}$,1),b>0,-1+a+b=0
∴1<a<2,g(x)=ex+2x-a在定义域内单调递增,
g(-$\frac{1}{2}$)=$\frac{1}{\sqrt{e}}$-1-a<0,
g(0)=1+0-a<0,
g($\frac{1}{2}$)=$\sqrt{e}$+2-a>0,
∴函数g(x)=lnx+f′(x)的零点所在的区间是(0,$\frac{1}{2}$);
故选:C.
点评 本题是中档题.考查导数的运算、函数零点的判断以及识图能力,体现了数形结合的思想,考查了学生应用知识分析解决问题的能力.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
10.设α∈(0,$\frac{π}{2}$),β∈(0,$\frac{π}{2}$),且tanα=$\frac{1}{7}$,tanβ=$\frac{1}{3}$,则α+2β=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
7.若数列{an}满足a1=1,an+1=an+2(n∈N*),则a4等于( )
| A. | 7 | B. | 9 | C. | 11 | D. | 13 |
12.要得到函数y=sin2x的图象,只需将函数y=sin(2x-2)的图象上的所有点沿x轴( )
| A. | 向左平移1个单位长度 | B. | 向左平移2个单位长度 | ||
| C. | 向右平移1个单位长度 | D. | 向右平移2个单位长度 |
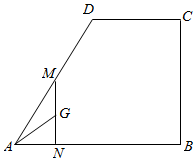 如图,梯形ABCD中,AB=AD=2CD=2,AB||CD,∠DAB=$\frac{π}{3}$,
如图,梯形ABCD中,AB=AD=2CD=2,AB||CD,∠DAB=$\frac{π}{3}$,