题目内容
设f(x)=
,则f(
)+(
)+f(
)+…+f(
)= .
| 4x |
| 4x+2 |
| 1 |
| 2014 |
| 2 |
| 2014 |
| 3 |
| 2014 |
| 2013 |
| 2014 |
考点:函数的值
专题:计算题,函数的性质及应用
分析:可求得f(x)+f(1-x)=1,运用该结论即可求得答案.
解答:
解:∵f(x)=
,
∴f(x)+f(1-x)=
+
=
+
=
+
=1,
∴f(
)+(
)+f(
)+…+f(
)\
=
{[f(
)+f(
)]+[f(
)+f(
)]+…+[f(
)+f(
)]+…+[f(
)+f(
)]}
=
(
)=
.
故答案为:
.
| 4x |
| 4x+2 |
∴f(x)+f(1-x)=
| 4x |
| 4x+2 |
| 41-x |
| 41-x+2 |
=
| 4x |
| 4x+2 |
| 4 |
| 4+2•4x |
=
| 4x |
| 4x+2 |
| 2 |
| 2+4x |
∴f(
| 1 |
| 2014 |
| 2 |
| 2014 |
| 3 |
| 2014 |
| 2013 |
| 2014 |
=
| 1 |
| 2 |
| 1 |
| 2014 |
| 2013 |
| 2014 |
| 2 |
| 2014 |
| 2012 |
| 2014 |
| 1007 |
| 2014 |
| 1007 |
| 2014 |
| 2013 |
| 2014 |
| 1 |
| 2014 |
=
| 1 |
| 2 |
| ||
| 2013个1 |
| 2013 |
| 2 |
故答案为:
| 2013 |
| 2 |
点评:该题考查函数值的求解,根据条件正确推导f(x)+f(1-x)=1是解决该题的关键所在.

练习册系列答案
相关题目
对于函数f(x)=sin2x+sinxcosx下列说法正确的是( )
| A、该函数的最小正周期为2π | ||||
| B、该函数为偶函数 | ||||
C、该函数的一个单调增区间为(-
| ||||
D、该函数图象的一个对称中心是(
|
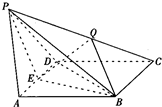 已知四棱锥P-ABCD中,底面ABCD是菱形,AB=PA=PD=2,∠ABD=
已知四棱锥P-ABCD中,底面ABCD是菱形,AB=PA=PD=2,∠ABD=