题目内容
9.设函数$f(x)=\left\{\begin{array}{l}{e^x}-a(x<1)\\ ln(x+a)(x≥1).\end{array}\right.$其中a>-1.①当a=0时,若f(x)=0,则x=1;
②若f(x)在(-∞,+∞)上是单调递增函数,则a的取值范围[ee-1-1,+∞).
分析 ①求出当a=0时的f(x)解析式,由f(x)=0,可得lnx=0,即可得到x的值;
②由题意可得a>-1,且e-1≤ln(1+a),解不等式即可得到所求范围.
解答 解:①当a=0时,f(x)=$\left\{\begin{array}{l}{{e}^{x},x<1}\\{lnx,x≥1}\end{array}\right.$,
由f(x)=0,可得lnx=0,解得x=1.
②若f(x)在(-∞,+∞)上是单调递增函数,
可得f(x)在x<1为递增,在x≥1为递增函数,
可得a>-1;
由增函数的定义可得e-1≤ln(1+a),
解得a≥ee-1-1.
综上可得a的范围是[ee-1-1,+∞).
故答案为:1,[ee-1-1,+∞).
点评 本题考查分段函数的运用,考查分段函数的自变量的求法和单调性的判断,注意运用指数函数和对数函数的单调性,考查运算能力,属于中档题.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
4.抛物线y=$\frac{1}{4}{x}^{2}$的准线方程为( )
| A. | x=-1 | B. | x=-$\frac{1}{16}$ | C. | y=-1 | D. | y=-$\frac{1}{16}$ |
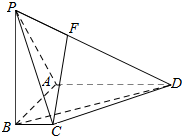 如图,在四棱锥P-ABCD中,PB⊥底面ABCD,底面ABCD为梯形,AD∥BC,AD⊥AB,且PB=AB=AD=3,BC=1.
如图,在四棱锥P-ABCD中,PB⊥底面ABCD,底面ABCD为梯形,AD∥BC,AD⊥AB,且PB=AB=AD=3,BC=1.