题目内容
已知|
|=3,|
|=4,向量+
与－的位置关系为（ ）
| A．平行 | B．垂直 | C．夹角为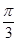 | D．不平行也不垂直 |
B
解析试题分析：因为||=3,||=4,所以（+）·（－）=
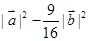=0，即向量+与－的位置关系为垂直，选B。
考点：本题主要考查平面向量的数量积，向量垂直的条件。
点评：简单题，两向量垂直，则它们的数量积为0.
练习册系列答案
世纪百通期末金卷系列答案
相关题目
点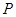
是
内一点且满足
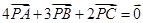，则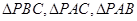
的面积比为（ ）
A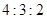． | B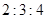． | C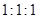． | D． |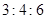
给出下列命题：
（1）两个具有公共终点的向量，一定是共线向量。
（2）两个向量不能比较大小，但它们的模能比较大小。
（3）
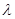a=0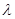（为实数），则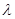必为零。
（4），
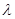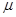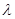为实数，若a=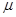b，则a与b共线。
其中错误的命题的个数为
| A．1 | B．2 | C．3 | D．4 |
已知
和点M满足
.若存在实数m使得
成立，则m= （ ）
| A．2 | B．3 | C．4 | D．5 |
设向量
，
，且
，则
等于
A． | B． | C． | D． |
已知
=（5，-3），C（-1，3），
=2，则点D的坐标为
| A．（11，9） | B．（4，0） | C．（9，3） | D．（9，-3） |
已知平面向量
，
，且
，则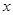
的值为（ ）
| A．－3 | B．-1 | C．1 | D．3 |
若四边形ABCD满足
，则该四边形一定不是 （ ）
| A．梯形 | B．菱形 | C．矩形 | D．正方形 |
已知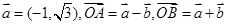
，若
是以点O为直角顶点的等腰直角三角形，则的面积为 （ ）
| A．2 | B．4 | C． | D． |