题目内容
设向量
，
，且
，则
等于
A． | B． | C． | D． |
D
解析试题分析：因为
， 所以
，所以
，故
.
考点：向量的共线
点评：本题考查向量共线定理的坐标形式，只要熟悉公式，直接套公式就可以，属基础题.
练习册系列答案
相关题目
设点M是线段BC的中点，点A在直线BC外，
，
则
=( )
| A．2 | B．4 | C．6 | D．8 |
已知圆
的半径为2，
是圆上两点且
，
是一条直径，点
在圆内且满足
，则
的最小值为（ ）
| A．－2 | B．－1 | C．－3 | D．－4 |
已知向量
表示“向东航行1km”，向量
表示“向南航行1km”，则向量
表示( )
A．向东南航行 km | B．向东南航行2km |
| C．向东北航行km | D．向东北航行2km |
P是
所在平面内一点，
，则P点一定在（ ）
| A．内部 | B．在直线AC上 |
| C．在直线AB上 | D．在直线BC上 |
已知|
|=3,|
|=4,向量+
与－的位置关系为（ ）
| A．平行 | B．垂直 | C．夹角为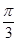 | D．不平行也不垂直 |
=（ ）
B. 
D. 
在空间四边形ABCD中，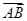
·
＋
·
＋
·
的值为( )
| A．0 | B． | C．1 | D．无法确定 |
已知向量a＝（1，2），a·b＝5，| a－b |＝
，则| b |等于
A． | B． | C．5 | D．25 |