题目内容
已知 和点M满足
和点M满足 .若存在实数m使得
.若存在实数m使得 成立,则m= ( )
成立,则m= ( )
| A.2 | B.3 | C.4 | D.5 |
B
解析试题分析:根据题意,由于 和点M满足
和点M满足 .则可知点M是三角形的重心,同时存在实数m使得
.则可知点M是三角形的重心,同时存在实数m使得 成立,则可知
成立,则可知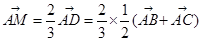 ,那么解得m=3,故答案为B.
,那么解得m=3,故答案为B.
考点:角平分线定理
点评:本试题主要考查向量的基本运算,考查角平分线定理

练习册系列答案
相关题目
设向量 ,若
,若 是实数,则
是实数,则 的最小值为( )
的最小值为( )
A. | B. | C.1 | D. |
已知 的外接圆半径为1,圆心为
的外接圆半径为1,圆心为 ,且
,且 0,则
0,则 的值为( )
的值为( )
A. | B. | C. | D. |
 +
+ -
- 等于( )
等于( )
A.2 | B.3 | C. | D. |
已知向量 表示“向东航行1km”,向量
表示“向东航行1km”,向量 表示“向南航行1km”,则向量
表示“向南航行1km”,则向量 表示( )
表示( )
A.向东南航行 km km | B.向东南航行2km |
C.向东北航行 km km | D.向东北航行2km |
设 、
、 、
、 是非零向量,则下列说法中正确是
是非零向量,则下列说法中正确是
A. | B. |
C.若 ,则 ,则 | D.若 ,则 ,则 |
已知| |=3,|
|=3,| |=4,向量
|=4,向量 +
+
 与
与 -
-
 的位置关系为( )
的位置关系为( )
| A.平行 | B.垂直 | C.夹角为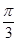 | D.不平行也不垂直 |
已知向量 夹角的取值范围是( )
夹角的取值范围是( )
A. | B. | C.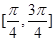 | D. |
若点M是 所在平面内的一点,且满足
所在平面内的一点,且满足 ,则
,则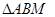 与
与 的面积比为( )
的面积比为( )
A. | B. | C. | D. |