题目内容
17.点A,B,C,D在格点图的位置如图所示,则向量$\overrightarrow{AD}$+$\overrightarrow{AC}$在$\overrightarrow{AB}$方向上的投影为( )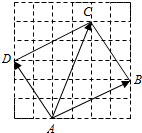
| A. | -$\frac{\sqrt{5}}{5}$ | B. | -$\frac{8\sqrt{5}}{5}$ | C. | $\frac{8\sqrt{5}}{5}$ | D. | 2 |
分析 利用向量$\overrightarrow{AD}$+$\overrightarrow{AC}$在$\overrightarrow{AB}$方向上的投影=$\frac{(\overrightarrow{AD}+\overrightarrow{AC})•\overrightarrow{AB}}{|\overrightarrow{AB}|}$,即可得出.
解答 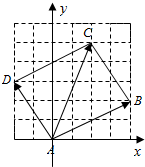 解:如图所示,A(0,0),B(4,2),C(2,5),D(-2,3).
解:如图所示,A(0,0),B(4,2),C(2,5),D(-2,3).
∴$\overrightarrow{AD}$=(-2,3),$\overrightarrow{AC}$=(2,5),$\overrightarrow{AB}$=(4,2).
∴$\overrightarrow{AD}+\overrightarrow{AC}$=(0,8).
∴向量$\overrightarrow{AD}$+$\overrightarrow{AC}$在$\overrightarrow{AB}$方向上的投影=$\frac{(\overrightarrow{AD}+\overrightarrow{AC})•\overrightarrow{AB}}{|\overrightarrow{AB}|}$=$\frac{16}{\sqrt{{4}^{2}+{2}^{2}}}$=$\frac{8\sqrt{5}}{5}$.
故选:C.
点评 本题考查了向量坐标运算、数量积运算性质、向量的投影,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
7.已知函数$f(x)=\frac{3^x}{{{3^x}+1}}$,正项等比数列{an}满足a1008=1,则f(lna1)+f(lna2)+f(lna3)+…+f(lna2015)=( )
| A. | 2015 | B. | $\frac{2015}{2}$ | C. | 2016 | D. | 1008 |
5.若0<m<n,则下列结论正确的是( )
| A. | log${\;}_{\frac{1}{2}}$m>log${\;}_{\frac{1}{2}}$n | B. | log2m>log2n | ||
| C. | ($\frac{1}{2}$)m<($\frac{1}{2}$)n | D. | 2m>2n |
2.“a2+b2=0”是“函数y=ax2+bx+c的图象关于原点中心对称“的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
2.下列求导运算正确的是( )
| A. | (x+$\frac{1}{x}$)′=1+$\frac{1}{x^2}$ | B. | (log3x)′=$\frac{1}{xln3}$ | C. | (5x)′=5xlog5e | D. | (x2cosx)′=2xsinx |
3.设直线nx+(n+1)y=$\sqrt{2}(n∈{N^*})$与两坐标轴围成的三角形面积为Sn,则S1+S2+S3+…S2013的值为( )
| A. | $\frac{2014}{2015}$ | B. | $\frac{2011}{2012}$ | C. | $\frac{2012}{2013}$ | D. | $\frac{2013}{2014}$ |
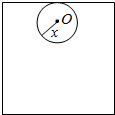 如图,半径为r的圆O在边长为4的正方形内与正方形一边相切并滚动一周后,圆O没有通过区域的面积为S.
如图,半径为r的圆O在边长为4的正方形内与正方形一边相切并滚动一周后,圆O没有通过区域的面积为S.