题目内容
椭圆
+y2=1和双曲线
-y2=1有相同的左、右焦点F1，F2，P是两曲线的一个交点，则|PF1|•|PF2|的值是 ．
| x2 |
| 4 |
| x2 |
| 2 |
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：设|PF1|=s，|PF2|=t，不妨取点P在双曲线的右支上．由双曲线和椭圆的定义可得可得s-t=2
，s+t=4，联立解得即可．
| 2 |
解答：
解：设|PF1|=s，|PF2|=t，不妨取点P在双曲线的右支上．
由题意可得s-t=2
，①s+t=4，②
由②2-①2得4st=8，
∴st=2．
故答案为：2．
由题意可得s-t=2
| 2 |
由②2-①2得4st=8，
∴st=2．
故答案为：2．
点评：本题考查了双曲线和椭圆的定义及其性质，属于中档题．
练习册系列答案
相关题目
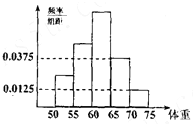为了了解某市今年准备报考体育专业的学生的体重情况，将所得的数据整理后，画出了频率分布直方图（如图），已知图中从左到右的前3个小组的频率之比为1：2：3，则第2小组的频率为
给出如图所示的数表序列．其中表i（i=1，2，3，…）有i行，表中每一个数“两脚”的两数都是此数的2倍，记表n中所有的数之和为an，例如a2=5，a3=17，a4=49，则an=
如图所示是某几何体的三视图，其中正视图是斜边为2的直角三角形，侧视图是半径为1的半圆，则该几何体的体积是