题目内容
9. 如图,四边形ABCD是正方形,PA⊥平面ABCD,PA=AB
如图,四边形ABCD是正方形,PA⊥平面ABCD,PA=AB(1)求证:PC⊥BD;
(2)求PC与平面ABCD所成角的余弦值.
分析 (1)连结AC,通过证明BD⊥平面PAC得出BD⊥PC;
(2)∠PCA为所求的线面角,设AB=PA=a,利用勾股定理计算出AC,PC即可解出.
解答 证明:(1)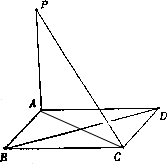 连结AC.
连结AC.
∵四边形ABCD是正方形,
∴BD⊥AC.
∵PA⊥平面ABCD,BD?平面ABCD,
∴PA⊥BD.
又PA?平面PAC,AC?平面PAC,PA∩AC=A,
∴BD⊥平面PAC,∵PC?平面PAC,
∴BD⊥PC.
(2)∵PA⊥平面ABCD,
∴∠PCA为直线PC与平面ABCD所成的角,
设PA=AB=a,
∵四边形ABCD是正方形,∴AC=$\sqrt{2}$AB=$\sqrt{2}a$.
∴PC=$\sqrt{P{A}^{2}+A{C}^{2}}$=$\sqrt{3}a$,
∴cos∠PCA=$\frac{AC}{PC}$=$\frac{\sqrt{2}a}{\sqrt{3}a}=\frac{\sqrt{6}}{3}$.
点评 本题考查了线面垂直的判定与性质,线面角的计算,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.已知函数f(x)的定义域为R,且f′(x)+f(x)=2xe-x,若f(0)=1,则函数$\frac{f′(x)}{f(x)}$的取值范围为( )
| A. | [-2,0] | B. | [-1,0] | C. | [0,1] | D. | [0,2] |
14.已知等差数列{an}中,a1+a12=12,则S12=( )
| A. | 24 | B. | 36 | C. | 72 | D. | 144 |