题目内容

已知椭圆C：
x2
2
+y2=1的左焦点为F，左准线为l，点A∈l，线段AF交椭圆C于点B，若
FA
=3
FB
，则|
AF
|=
 
．
分析：先根据
FA
=3
FB
推断出
|AB|
|BF|
=
2
3
，B点到直线L的距离设为BE，则利用椭圆方程中的a，b求得c，可求得||BF|，进而求得|BE|，进而根据椭圆的第二定义求得BF的长，则根据
FA
=3
FB
求得|
AF
|．
解答：解：由条件，∵
FA
=3
FB

∴
|AB|
|BF|
=
2
3
 
B点到直线L的距离设为BE，则
|BE|
a2
c
-c
=
2
3

∴|BE|=
2
3

根据椭圆定义e=
1
2
=
|BF|
|BE|
 从而求出|BF|=
2
3
2

∴|
AF
|=
2
3
2
×3=
2

故答案为
2
．
点评：本题主要考查了椭圆的应用．解题中灵活利用了椭圆的第二定义，是解题的关键．
练习册系列答案
相关题目
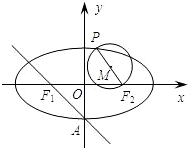已知椭圆C：
x2
2
+y2=1的两焦点为F1，F2，点P（x0，y0）满足0＜
x
2
0
2
+
y
2
0
＜1，则|PF1|+PF2|的取值范围为
 
，直线
x0x
2
+y0y=1与椭圆C的公共点个数
 
．
已知椭圆C：
x2
2
+y2=1的右焦点为F，右准线为l，点A∈l，线段AF交C于点B，若
FA
=3
FB
，则|
AF
|=（　　）
A、
2
B、2
C、
3
D、3
精英家教网已知椭圆C：
x2
2
+y2=1的左、右焦点分别为F1，F2，下顶点为A，点P是椭圆上任一点，⊙M是以PF2为直径的圆．
（Ⅰ）当⊙M的面积为
π
8
时，求PA所在直线的方程；
（Ⅱ）当⊙M与直线AF1相切时，求⊙M的方程；
（Ⅲ）求证：⊙M总与某个定圆相切．
已知椭圆C：
x2
2
+y2=1的右焦点为F，直线l：x=2，点A∈l，线段AF交C于点B，若
FA
=3
FB
，则|
AF
|=（　　）
（2011•许昌三模）已知椭圆C：
x2
2
+y2=1的左右焦点分别为F1、F2，下顶点为A，点P是椭圆上任意一点，圆M是以PF2为直径的圆．
（I）当圆M的面积为
π
8
时，求PA所在直线的方程；
（Ⅱ）当圆M与直线AF1相切时，求圆M的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网