题目内容
16.在△ABC中,若acosA=bcosB,C=60°,则△ABC的形状为( )| A. | 等腰三角形 | B. | 直角三角形 | ||
| C. | 等边三角形 | D. | 等腰三角形或直角三角形 |
分析 由余弦定理得c2(a2-b2)=(a2-b2)(a2+b2),由C=60°,得到△ABC为等边三角形.
解答 解:∵在△ABC中,acosA=bcosB,
∴由余弦定理得:$a×\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}=b×\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$,
整理,得c2(a2-b2)=(a2-b2)(a2+b2),
∵C=60°,
∴a=b=c,
∴△ABC的形状为等边三角形.
故选:C.
点评 本题考查三角形形状的判断,考查余弦定理、三角形性质等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.设双曲线的左右两个焦点分别为F1,F2,过F2作双曲线实轴的垂线交双曲线于点P,若△F1PF2为等腰直角三角形,则双曲线的离心率是( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}+1}{2}$ | C. | 2$+\sqrt{2}$ | D. | 1$+\sqrt{2}$ |
4.已知三棱柱ABC-A1B1C1的底面ABC是边长为1的正三角形,侧棱AA1与底面所成的角是60°,在侧棱AA1,BB1,CC1上分别有点P,Q,R且AP=$\frac{3}{2}$,BQ=1,CR=$\frac{1}{2}$,则截面PQR与底面ABC之间的几何体的体积是( )
| A. | $\frac{3}{8}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{\sqrt{3}}{2}$ |
 的左、右焦点分别为
的左、右焦点分别为 ,椭圆
,椭圆 过点
过点 ,直线
,直线 交
交 轴于
轴于 ,且
,且 ,
,  为坐标原点.
为坐标原点.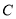 的方程;
的方程;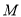 是椭圆
是椭圆 的上顶点,过点
的上顶点,过点 分别作直线
分别作直线 交椭圆
交椭圆 于
于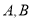 两点,设这两条直线的斜率分别为
两点,设这两条直线的斜率分别为 ,且
,且 ,证明:直线
,证明:直线 过定点.
过定点. ,那么
,那么 是( )
是( ) B.
B.
 D.
D.
 是
是 上的偶函数,且在
上的偶函数,且在 上是增函数,若
上是增函数,若 ,则
,则 的解集是 .
的解集是 . 的抛物线的标准方程为 .
的抛物线的标准方程为 .