题目内容
7.已知i为虚数单位,复数z=a+i(a<0),且|z|=$\sqrt{10}$,则复数z的实部为( )| A. | 3 | B. | -3 | C. | -1 | D. | i |
分析 利用复数模的公式得到关于a的方程,求解方程得答案.
解答 解:∵z=a+i(a<0),且|z|=$\sqrt{10}$,
∴$\sqrt{{a}^{2}+1}=\sqrt{10}$,即a2+1=10,
则a2=9,
∴a=-3.
故选:B.
点评 本题考查复数模的求法,是基础的计算题.

练习册系列答案
相关题目
17.下列说法正确的是( )
| A. | P(B|A)<P(AB) | B. | P(B|A)=$\frac{P(B)}{P(A)}$是可能的 | ||
| C. | 0<P(B|A)<1 | D. | P(A|A)=0 |
15.已知函数f(x)=2x2+3,g(x)=a$\sqrt{{x}^{2}+1}$,若对于任意的x∈R,f(x)>g(x)恒成立,则实数a的取值范围是( )
| A. | (-∞,2$\sqrt{2}$) | B. | (-∞,2$\sqrt{2}$] | C. | (-∞,3) | D. | (-∞,3] |
12.在不等式组$\left\{\begin{array}{l}0≤x≤2\\ 0≤y≤2\end{array}\right.$表示的平面区域内任取一个点P(x,y),使得x+y≤1的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{12}$ |
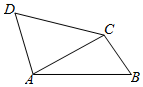 如图,△ABC中,AB=4,BC=2,∠ABC=∠D=60°,△ADC是锐角三角形,DA+DC的取值范围为$(6,4\sqrt{3}]$.
如图,△ABC中,AB=4,BC=2,∠ABC=∠D=60°,△ADC是锐角三角形,DA+DC的取值范围为$(6,4\sqrt{3}]$.