题目内容
某单位有8个连在一起的车位，现有4辆不同型号的车需要停放，如果要求剩余的四个空位各不相连，则不同的停车方法有（ ）
| A、48种 | B、96种 |
| C、120种 | D、144种 |
考点：计数原理的应用
专题：应用题,排列组合
分析：分两类：4辆不同型号的车各不相连，则有2
=48种；辆不同型号的车有两辆相连，则有
=72种，即可得出结论．
| A | 4 4 |
| C | 2 4 |
| A | 3 3 |
| A | 2 2 |
解答：
解：由题意，若4辆不同型号的车各不相连，则有2
=48种；
若4辆不同型号的车有两辆相连，则有
=72种；
∴不同的停车方法有48+72=120种．
古选：C．
| A | 4 4 |
若4辆不同型号的车有两辆相连，则有
| C | 2 4 |
| A | 3 3 |
| A | 2 2 |
∴不同的停车方法有48+72=120种．
古选：C．
点评：本题考查排列组合的实际应用，解题的关键是正确分类．
练习册系列答案
学而优暑期衔接南京大学出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
设
，
，
是任意的非零向量，且相互不共线，则
（1）(
•
)
-(
•
)
=0；
（2）若
•
=
•
，则
=
；
（3）|
|-|
|＜|
-
|；
（4）（3
+2
）•（3
-2
）=9|
|2-4|
|2；
其中是真命题的有（ ）
| a |
| b |
| c |
（1）(
| a |
| b |
| c |
| c |
| a |
| b |
（2）若
| a |
| b |
| a |
| c |
| b |
| c |
（3）|
| a |
| b |
| a |
| b |
（4）（3
| a |
| b |
| a |
| b |
| a |
| b |
其中是真命题的有（ ）
| A、（1）（2） |
| B、（2）（3） |
| C、（3）（4） |
| D、（2）（4） |
已知
=（sinα，cosα），
=（sin
，cos
），且
⊥
，则符合要求的α为（ ）
| a |
| b |
| π |
| 4 |
| π |
| 4 |
| a |
| b |
A、
| ||
B、-
| ||
C、
| ||
D、
|
化简式子cos82°cos22°+sin82°sin22°的值是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
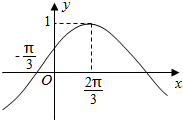已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜| π |
| 2 |
A、f（x）=2sin（
| ||||
B、f（x）=2sin（
| ||||
C、f（x）=sin（
| ||||
D、f（x）=sin（
|
有四个关于三角函数的命题，其中所有真命题的序号是（ ）
①存在x∈R，使sin2
+cos2
=
②存在x∈R，使sin（x-y）=sinx-siny
③存在x∈（0，π），使
=sinx
④在△ABC中，A＞B?sinA＞sinB．
①存在x∈R，使sin2
| x |
| 2 |
| x |
| 2 |
| 1 |
| 2 |
②存在x∈R，使sin（x-y）=sinx-siny
③存在x∈（0，π），使
|
④在△ABC中，A＞B?sinA＞sinB．
| A、②③ | B、③④ |
| C、②③④ | D、①②④ |
要得到函数f（x）=-
f（
-x）-sinx的图象，只需将g（x）=sinx的图象（ ）
| 3 |
| π |
| 2 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
