题目内容
3．
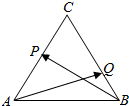如图，在△ABC中，已知$\overrightarrow{AP}$=$\overrightarrow{PC}$，$\overrightarrow{CQ}$=2$\overrightarrow{QB}$，设$\overrightarrow{BP}$=m•$\overrightarrow{AB}$+n•$\overrightarrow{AC}$．（1）求m+n的值；
（2）已知|$\overrightarrow{AB}$|=c，|$\overrightarrow{AC}$|=b，求$\overrightarrow{AQ}$•$\overrightarrow{BP}$．
分析 （1）用$\overrightarrow{AB}，\overrightarrow{AC}$表示出$\overrightarrow{BP}$，求出m，n的值；
（2）用$\overrightarrow{AB}，\overrightarrow{AC}$表示出$\overrightarrow{AQ}$，计算数量级．
解答 解：（1）$\overrightarrow{BP}=\overrightarrow{BC}+\overrightarrow{CP}$=$\overrightarrow{AC}-\overrightarrow{AB}-\frac{1}{2}\overrightarrow{AC}$=-$\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}$，
∴m=-1，n=$\frac{1}{2}$．∴m+n=-$\frac{1}{2}$．
（2）$\overrightarrow{AQ}$=$\overrightarrow{AB}+\overrightarrow{BQ}$=$\overrightarrow{AB}+\frac{1}{3}\overrightarrow{BC}$=$\overrightarrow{AB}+\frac{1}{3}（\overrightarrow{AC}-\overrightarrow{AB}）$=$\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$，
∴$\overrightarrow{AQ}$•$\overrightarrow{BP}$=（$\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$）•（-$\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}$）=-$\frac{2}{3}$$\overrightarrow{AB}$2+$\frac{1}{3}$$\overrightarrow{AB}•\overrightarrow{AC}$-$\frac{1}{3}\overrightarrow{AC}•\overrightarrow{AB}$+$\frac{1}{6}$$\overrightarrow{AC}$2=-$\frac{2}{3}$c2+$\frac{1}{6}$b2．
点评 本体考查了平面向量的三角形法则和数量级运算，属于基础题．
| A． | “若$\overrightarrow a•\overrightarrow b=0$，则$\overrightarrow a⊥\overrightarrow b$”的否命题是“若$\overrightarrow a•\overrightarrow b≠0$，则$\overrightarrow a⊥\overrightarrow b$” | |
| B． | 命题“?x∈R，恒有x2+1＞0”的否定是“?x0∈R，使得${x_0}^2+1＜0$” | |
| C． | ?m∈R，使函数f（x）=x2+mx（x∈R）是奇函数 | |
| D． | 设p，q是简单命题，若p∧q是真命题，则（￢p）∨q也是真命题 |