题目内容
已知x∈R，等式
=1成立的充要条件是 ．
| |x| |
| x |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：当x＞0时，等式
=1恒成立，当x≤0时，等式
=1不成立，即可得出．
| |x| |
| x |
| |x| |
| x |
解答：
解：当x＞0时，等式
=1恒成立，当x≤0时，等式
=1不成立．
因此等式
=1成立的充要条件是x＞0．
故答案为：x＞0．
| |x| |
| x |
| |x| |
| x |
因此等式
| |x| |
| x |
故答案为：x＞0．
点评：本题考查了分类讨论的思想方法、充要条件的判定，属于基础题．
练习册系列答案
相关题目
设α、β为两个不同的平面，m、n为两条不同的直线，则a⊥b的一个充分条件是（ ）
| A、a⊥α，b∥β，α⊥β |
| B、a⊥α，b⊥β，α∥β |
| C、a?α，b⊥β，α∥β |
| D、a?α，b∥β，α⊥β |
“0＜k＜9”是“曲线
-
=1与曲线
-
=1的焦距相同”的（ ）
| x2 |
| 25 |
| y2 |
| 9-k |
| x2 |
| 25-k |
| y2 |
| 9 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
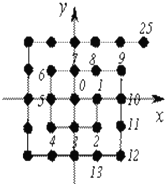将平面直角坐标系中的格点（横、纵坐标均为整数的点）按如下规则标上数字标签：原点处标0，点（1，0）处标1，点（1，-1）处标2，点（0，-1）处标3，点（-1，-1）处标4，…，点（0，1）处标7，…，依此类推，则标签20152的格点的坐标为（ ）| A、（1008，1007） |
| B、（1007，1006） |
| C、（1007，1005） |
| D、（1006，1005） |
在四边形ABCD中，下列是映射的是（ ）
| A、1、2、3 | B、1、2 |
| C、1、3 | D、2、3 |