Question

若椭圆C：

x2

a2

+

y2

b2

=1(a＞b＞0)的焦距为2

5

，且过点（-3，2），⊙O的圆心为原点，直径为椭圆的短轴，⊙M的方程为（x-8）²+（y-6）²=4，过⊙M上任一点P作⊙O的切线PA、PB，切点为A、B．
（1）求椭圆的方程；
（2）若直线PA与⊙M的另一交点为Q，当弦PQ最大时，求直线PA的直线方程；
（3）求

OA

•

OB

的最大值．

Answer 1

（1）由椭圆C：

x2

a2

+

y2

b2

=1(a＞b＞0)的焦距为2

5

，且过点（-3，2），∴

9 a2 + 4 b2 =1 2c=2 5 a2=b2+c2

，
解得

c= 5 b2=10 a2=15

，
∴椭圆的方程为

x2

15

+

y2

10

=1．
（2）∵⊙O的圆心为原点，直径为椭圆的短轴，∴⊙O的方程为x²+y²=10．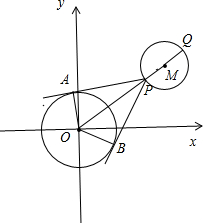
当弦PQ最大时，即PQ是⊙M的直径，
设直线PA的方程为y-6=k（x-8），即kx-y+6-8k=0．
∵直线PA与⊙O相切，∴点O到直线PA的距离d=

10

，
∴

|6-8k|

k2+1

=

10

，解得k=

1

3

或

13

9

．
∴直线PA的方程为

1

3

x-y+6-

8

3

=0，或

13

9

x-y+6-

104

9

=0，
化为x-3y+10=0，或13x-9y-50=0．
（3）设∠AOB=2θ，∵θ∈(0，

π

2

)，∴2θ∈（0，π）．

OA

•

OB

=|

OA

||

OB

|cos∠AOB=10cos2θ，
∵2θ∈（0，π），∴cos2θ在θ∈(0，

π

2

)上单调递减，
因此当θ取得最小值时，cos2θ取得最大值．
∵cosθ=

10

OP

，∴当OP取得最小值时，cosθ取得最大值．
当P点取OM与⊙M的交点时，OP取得最小值．
又|OP|=|OM|-2=

62+82

-2=8．
∴cosθ=

10

8

，cos2θ=2cos²θ-1=-

11

16

．
∴

OA

•

OB

取得最大值10×(-

11

16

)=-

55

8

．