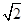题目内容
已知双曲线C的渐近线为y=±
x且过点M(1,
).
(1)求双曲线C的方程;
(2)若直线y=ax+1与双曲线C相交于A,B两点,O为坐标原点,若OA与OB垂直,求a的值.
| 3 |
| 2 |
(1)求双曲线C的方程;
(2)若直线y=ax+1与双曲线C相交于A,B两点,O为坐标原点,若OA与OB垂直,求a的值.
(1)由题意可知:双曲线的焦点在x轴上,可设方程为
-
=1,
则
,解得
,
∴双曲线C的方程为3x2-y2=1.
(2)设A(x1,y1),B(x2,y2),联立
,化为(3-a2)x2-2ax-2=0,(3-a2≠0).
∵直线y=ax+1与双曲线C相交于A,B两点,∴△=4a2+8(3-a2)>0,化为a2<6.
∴x1+x2=
,x1x2=
.(*)
∵
⊥
,∴
•
=0.
∴x1x2+y1y2=0,又y1=ax1+1,y2=ax2+1,
∴(1+a2)x1x2+a(x1+x2)+1=0,
把(*)代入上式得
+
+1=0,
化为a2=1.满足△>0.
∴a=±1.
| x2 |
| a2 |
| y2 |
| b2 |
则
|
|
∴双曲线C的方程为3x2-y2=1.
(2)设A(x1,y1),B(x2,y2),联立
|
∵直线y=ax+1与双曲线C相交于A,B两点,∴△=4a2+8(3-a2)>0,化为a2<6.
∴x1+x2=
| 2a |
| 3-a2 |
| -2 |
| 3-a2 |

∵
| OA |
| OB |
| OA |
| OB |
∴x1x2+y1y2=0,又y1=ax1+1,y2=ax2+1,
∴(1+a2)x1x2+a(x1+x2)+1=0,
把(*)代入上式得
| -2(1+a2) |
| 3-a2 |
| 2a2 |
| 3-a2 |
化为a2=1.满足△>0.
∴a=±1.

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
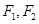 为椭圆E的两个左右焦点,抛物线C以
为椭圆E的两个左右焦点,抛物线C以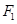 为顶点,
为顶点,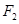 为焦点,设P为椭圆与抛物线的一个交点,如果椭圆离心率e满足
为焦点,设P为椭圆与抛物线的一个交点,如果椭圆离心率e满足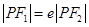 ,则e的值为( )
,则e的值为( )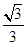 B.
B.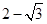 C.
C. 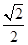 D.
D.