题目内容
若点O和点F分别为椭圆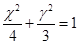 的中心和左焦点,点P为椭圆上的任意一点,则
的中心和左焦点,点P为椭圆上的任意一点,则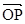 ·
·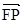 的最大值为( ).
的最大值为( ).
| A.2 | B.3 | C.6 | D.8 |
C
解析试题分析:由题意,F(-1,0),设点P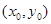 ,则有
,则有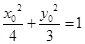 ,解得
,解得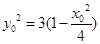 ,
,
因为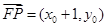 ,
,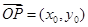 ,所以
,所以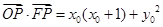
=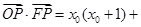
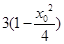 =
=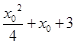 ,此二次函数对应的抛物线的对称轴为
,此二次函数对应的抛物线的对称轴为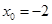 ,因为
,因为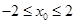 ,所以当
,所以当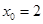 时,
时, 取得最大值
取得最大值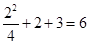 ,选C
,选C
考点:本题考查了椭圆与数量积的运算
点评:此类问题比较综合,考查了椭圆的方程、几何性质、平面向量的数量积的坐标运算、二次函数的单调性与最值等,考查了同学们对基础知识的熟练程序以及知识的综合应用能力、运算能力

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
已知双曲线 的两条渐近线均与
的两条渐近线均与 相切,则该双曲线离心率等于( )
相切,则该双曲线离心率等于( )
A. | B. | C. | D. |
过点 且与抛物线
且与抛物线 只有一个公共点的直线有( ).
只有一个公共点的直线有( ).
A. 条 条 | B. 条 条 | C.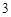 条 条 | D. 条 条 |
抛物线 的焦点为
的焦点为 ,点
,点 为抛物线上的动点,点
为抛物线上的动点,点 为其准线上的动点,当
为其准线上的动点,当 为等边三角形时,其面积为
为等边三角形时,其面积为
A. | B.4 | C.6 | D.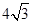 |
若双曲线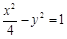 的渐近线与圆
的渐近线与圆 (
(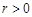 )相切,则
)相切,则
| A.5 | B.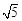 | C.2 | D. |
已知动点 在椭圆
在椭圆 上,若
上,若 点坐标为
点坐标为 ,
, ,且
,且 ,则
,则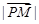 的最小值是( )
的最小值是( )
A. | B. | C. | D. |
若双曲线 的离心率是2,则实数k的值是 ( )
的离心率是2,则实数k的值是 ( )
| A.—3 | B.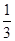 | C.3 | D.—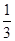 |
设 、
、 是双曲线
是双曲线 的左、右两个焦点,若双曲线右支上存在一点P,使
的左、右两个焦点,若双曲线右支上存在一点P,使 ,且
,且 ,则
,则 的值为( )
的值为( )
| A.2 | B. | C.3 | D. |
过双曲线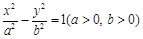 左焦点
左焦点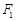 的直线与以右焦点
的直线与以右焦点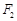 为圆心、
为圆心、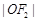 为半径的圆相切于A点,且
为半径的圆相切于A点,且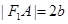 ,则双曲线的离心率为
,则双曲线的离心率为
A.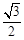 | B.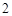 | C.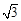 | D. |